To com 2 dúvidas aqui de conjuntos, que queria explicação.
1) Se A = { x
 N / x = 4n, com n
N / x = 4n, com n  N} e B = { x
N} e B = { x  N* /
N* /  = n, com n
= n, com n  N}
N}Então o nº de elementos de A
 B é:
B é:b)2 elementos.
Bom, eu não entendi muito bem o que o exercício quer, pelo que entendi o conjunto A é dos múltiplos de 4 (4, 8, 12, 16, 20...) e B os divisores de 20?
2)O número de elementos do conjunto P(A)
 P(B), com A e B disjuntos e com dois elementos cada um é:
P(B), com A e B disjuntos e com dois elementos cada um é:d) 7
.
Tbm não sei como vou achar o número de elementos, se tem 2 elementos cada um então a união deles não seriam 4 elementos???Pq tem 7? e como eu leio isso :P(A)
Outra coisa : como to estudando pelas aulas do Nerckie, ele não dá aula de intervalo e aborda o assunto só depois de Funções...Vcs acham que é bom eu pegar intervalo agora ou seguir pela sequência que ele dá?
Conto com vcs





 significa os múltiplos de 4 enquanto que
significa os múltiplos de 4 enquanto que  representa os divisores de 20. Daí, basta ver elementos em comum.
representa os divisores de 20. Daí, basta ver elementos em comum. você quer dizer o número de subconjuntos de
você quer dizer o número de subconjuntos de 

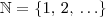 , então escreveu certo.
, então escreveu certo.
 . Tanto é assim, que na definição do conjunto
. Tanto é assim, que na definição do conjunto  , indicando que nesse caso devemos tirar o 0 de
, indicando que nesse caso devemos tirar o 0 de 

 .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.