 por Andrewo » Qui Abr 12, 2012 09:12
por Andrewo » Qui Abr 12, 2012 09:12
Aí rapaziada; blza?
To com 2 dúvidas aqui de conjuntos, que queria explicação.
1) Se A = { x  N / x = 4n, com n
N / x = 4n, com n  N} e B = { x
N} e B = { x  N* /
N* /  = n, com n
= n, com n  N}
N}
Então o nº de elementos de A B é:
B é:
b)2 elementos.Bom, eu não entendi muito bem o que o exercício quer, pelo que entendi o conjunto A é dos múltiplos de 4 (4, 8, 12, 16, 20...) e B os divisores de 20?
2)O número de elementos do conjunto P(A)  P(B), com A e B disjuntos e com dois elementos cada um é:
P(B), com A e B disjuntos e com dois elementos cada um é:
d) 7.
Tbm não sei como vou achar o número de elementos, se tem 2 elementos cada um então a união deles não seriam 4 elementos???Pq tem 7? e como eu leio isso :P(A)
Outra coisa : como to estudando pelas aulas do Nerckie, ele não dá aula de intervalo e aborda o assunto só depois de Funções...Vcs acham que é bom eu pegar intervalo agora ou seguir pela sequência que ele dá?
Conto com vcs



-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Abr 12, 2012 19:36
por MarceloFantini » Qui Abr 12, 2012 19:36
No primeiro você interpretou corretamente, o conjunto

significa os múltiplos de 4 enquanto que

representa os divisores de 20. Daí, basta ver elementos em comum.
Com a notação

você quer dizer o número de subconjuntos de

? De onde tirou a questão?
Para responder à questão do intervalo precisamos saber se é um estudo sozinho ou se você depende deste conhecimento para algum assunto urgente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Andrewo » Sex Abr 13, 2012 09:08
por Andrewo » Sex Abr 13, 2012 09:08
MarceloFantini escreveu:Com a notação

você quer dizer o número de subconjuntos de

? De onde tirou a questão?
Para responder à questão do intervalo precisamos saber se é um estudo sozinho ou se você depende deste conhecimento para algum assunto urgente.
Tirei de uma lista de exercícios de vestibular, é questão da UFRS.
Quanto ao estudo, eu estudo sozinho sim, e quero estudar a matéria toda do ensino médio p/ fazer uma prova daqui a 2,5 meses.




-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sex Abr 13, 2012 10:22
por LuizAquino » Sex Abr 13, 2012 10:22
Você esqueceu do 0 no conjunto A. Ou seja, lembre-se que 0 é múltiplo de 4.
Andrewo escreveu:2)O número de elementos do conjunto P(A)

P(B), com A e B disjuntos e com dois elementos cada um é:
d) 7
Andrewo escreveu:Tbm não sei como vou achar o número de elementos, se tem 2 elementos cada um então a união deles não seriam 4 elementos??
De modo geral, se dois conjuntos A e B possuem 2 elementos, não necessariamente a união deles terá 4 elementos. Por exemplo, considere os conjuntos A = {1, 2} e B = {2, 3}. Fazendo a união de A com B, por acaso teríamos 4 elementos?
Entretanto, no caso do exercício, os conjuntos A e B são disjuntos. Você sabe o que isso significa? Caso você não saiba, vide, por exemplo, a página:
Conjuntos disjuntoshttp://pt.wikipedia.org/wiki/Conjuntos_disjuntosAndrewo escreveu:Pq tem 7? e como eu leio isso :P(A)
Para entender o porque da resposta ser 7, você precisa primeiro saber o que significa P(A). Para saber o que isso significa, vide, por exemplo, a página:
Conjunto de partes http://pt.wikipedia.org/wiki/Conjunto_de_partesAndrewo escreveu:Quanto ao estudo, eu estudo sozinho sim, e quero estudar a matéria toda do ensino médio p/ fazer uma prova daqui a 2,5 meses.
Uma curiosidade: será uma prova de vestibular ou de concurso?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Abr 13, 2012 10:58
por MarceloFantini » Sex Abr 13, 2012 10:58
Luiz, considerar 0 como múltiplo depende da convenção dos números naturais que ele esteja usando. Caso seja
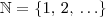
, então escreveu certo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Andrewo » Sex Abr 13, 2012 11:44
por Andrewo » Sex Abr 13, 2012 11:44
LuizAquino escreveu:Andrewo escreveu:Andrewo escreveu:Tbm não sei como vou achar o número de elementos, se tem 2 elementos cada um então a união deles não seriam 4 elementos??
De modo geral, se dois conjuntos A e B possuem 2 elementos, não necessariamente a união deles terá 4 elementos. Por exemplo, considere os conjuntos A = {1, 2} e B = {2, 3}. Fazendo a união de A com B, por acaso teríamos 4 elementos?
Entretanto, no caso do exercício, os conjuntos A e B são disjuntos. Você sabe o que isso significa? Caso você não saiba, vide, por exemplo, a página:
Para entender o porque da resposta ser 7, você precisa primeiro saber o que significa P(A). Para saber o que isso significa, vide, por exemplo, a página:
Conjunto de partes http://pt.wikipedia.org/wiki/Conjunto_de_partesAndrewo escreveu:Quanto ao estudo, eu estudo sozinho sim, e quero estudar a matéria toda do ensino médio p/ fazer uma prova daqui a 2,5 meses.
Uma curiosidade: será uma prova de vestibular ou de concurso?
Eu ja sabia o que eram disjuntos mas não sabia que P(a) significava conjunto de partes.
Mas mesmo assim o resultado não bate pq se eu for ver o conjunto de partes de P(a) = 4 e de P(b) = 4 tbm, o enunciado não fala nada em partes não vazias, então o resultado correto não seria 8?
É prova de vestibular.

-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sex Abr 13, 2012 11:48
por LuizAquino » Sex Abr 13, 2012 11:48
MarceloFantini escreveu:Luiz, considerar 0 como múltiplo depende da convenção dos números naturais que ele esteja usando. Caso seja
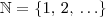
, então escreveu certo.
Esse exercício foi proposto a nível de Matemática do ensino fundamental e médio. Nesse caso, o número 0 pertence a

. Tanto é assim, que na definição do conjunto
B note que aparece

, indicando que nesse caso devemos tirar o 0 de

.
Andrewo escreveu:Eu ja sabia o que eram disjuntos mas não sabia que P(a) significava conjunto de partes.
Mas mesmo assim o resultado não bate pq se eu for ver o conjunto de partes de P(a) = 4 e de P(b) = 4 tbm, o enunciado não fala nada em partes não vazias, então o resultado correto não seria 8?
Faço o teste. Considere que A = {1, 2} e B = {3, 4}. Note que esses conjuntos são disjuntos.
Determinando o conjunto das partes, temos que:


Agora conte quantos elementos tem

.
Editado pela última vez por
LuizAquino em Sex Abr 13, 2012 11:53, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Abr 13, 2012 11:50
por MarceloFantini » Sex Abr 13, 2012 11:50
Andrewo, não se esqueça que o vazio é um elemento em comum a ambos e quando contamos elementos de um conjunto não consideramos repetidos, por isso apenas sete.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas - Conjuntos
por joaopedrel » Sáb Mar 13, 2010 23:06
- 2 Respostas
- 2135 Exibições
- Última mensagem por joaopedrel

Dom Mar 14, 2010 19:54
Conjuntos
-
- [Diferença de Conjuntos] Dúvidas!
por Young » Sáb Set 06, 2008 15:42
- 1 Respostas
- 5478 Exibições
- Última mensagem por admin

Ter Set 09, 2008 16:11
Álgebra Elementar
-
- [Conjuntos] Dúvidas no exercício.
por HeidyTrinidad » Sex Abr 11, 2014 10:35
- 1 Respostas
- 1803 Exibições
- Última mensagem por e8group

Sex Abr 11, 2014 18:16
Conjuntos
-
- Dúvidas Teoria dos Conjuntos
por GabrielSilv0 » Seg Set 21, 2015 14:59
- 1 Respostas
- 1615 Exibições
- Última mensagem por nakagumahissao

Dom Out 04, 2015 12:59
Conjuntos
-
- Tenho dúvidas de como resolver este exercício de conjuntos
por Thiago Sousa » Ter Mai 06, 2008 17:11
- 2 Respostas
- 4573 Exibições
- Última mensagem por Thiago Sousa

Ter Mai 06, 2008 19:25
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 N / x = 4n, com n
N / x = 4n, com n  N} e B = { x
N} e B = { x  N* /
N* /  = n, com n
= n, com n  N}
N} B é:
B é: P(B), com A e B disjuntos e com dois elementos cada um é:
P(B), com A e B disjuntos e com dois elementos cada um é:




 significa os múltiplos de 4 enquanto que
significa os múltiplos de 4 enquanto que  representa os divisores de 20. Daí, basta ver elementos em comum.
representa os divisores de 20. Daí, basta ver elementos em comum. você quer dizer o número de subconjuntos de
você quer dizer o número de subconjuntos de 

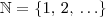 , então escreveu certo.
, então escreveu certo.
 . Tanto é assim, que na definição do conjunto
. Tanto é assim, que na definição do conjunto  , indicando que nesse caso devemos tirar o 0 de
, indicando que nesse caso devemos tirar o 0 de 

 .
.




