


 , isto é, a soma de n+1 termos menos a soma de n termos.
, isto é, a soma de n+1 termos menos a soma de n termos.

MarceloFantini escreveu:Isso é provavelmente a soma da sequência e não o termo geral.
Dica: para encontrar cada termo, faça, isto é, a soma de n+1 termos menos a soma de n termos.

 . Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de
. Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de  , sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos
, sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos  encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo
encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo  .
.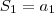 ,
,  ,
,  , e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
, e assim em diante. Usando o método que expliquei acima, você chegará na resposta.

 . Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de
. Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de  , sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos
, sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos  encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo
encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo  .
.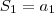 ,
,  ,
,  , e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
, e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
 , use isso juntamente com o que eu disse.
, use isso juntamente com o que eu disse.

MarceloFantini escreveu:O enunciado parece ter dito que o valor da soma de N termos é, use isso juntamente com o que eu disse.

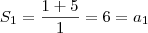 .
.  , logo
, logo 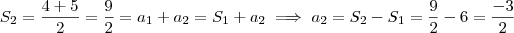 .
. 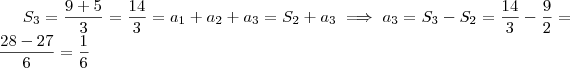 .
. 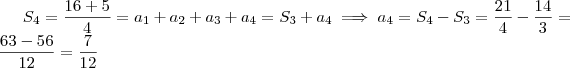 .
.por favor me ajudem na sequencia definida por an=n²+5 dividido por n, escrver os 5 primeiros termos da pa.


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes