 por matem » Ter Nov 29, 2011 17:07
por matem » Ter Nov 29, 2011 17:07
por favor me ajudem na sequencia definida por an=n²+5 dividido por n, escrver os 5 primeiros termos da pa.
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Ter Nov 29, 2011 19:12
por MarceloFantini » Ter Nov 29, 2011 19:12
Isso é provavelmente a
soma da sequência e não o termo geral.
Dica: para encontrar cada termo, faça

, isto é, a soma de n+1 termos menos a soma de n termos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matem » Ter Nov 29, 2011 21:28
por matem » Ter Nov 29, 2011 21:28
MarceloFantini escreveu:Isso é provavelmente a
soma da sequência e não o termo geral.
Dica: para encontrar cada termo, faça

, isto é, a soma de n+1 termos menos a soma de n termos.
NÃO ENTENDI NADA SE POSSIVEL EXPLICAR PASSO A PASSO
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Qua Nov 30, 2011 00:21
por MarceloFantini » Qua Nov 30, 2011 00:21
Suponha que você tem uma soma de 5 termos

. Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de

, sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos

encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo

.
No caso do exercício, é análogo. Ele te dá a soma de uma quantidade arbitrária, n, de elementos. Ele quer que você encontre os cinco primeiros termos da sequência. Perceba que
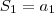
,

,

, e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matem » Qua Nov 30, 2011 21:42
por matem » Qua Nov 30, 2011 21:42
[quote="MarceloFantini"]Suponha que você tem uma soma de 5 termos

. Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de

, sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos

encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo

.
No caso do exercício, é análogo. Ele te dá a soma de uma quantidade arbitrária, n, de elementos. Ele quer que você encontre os cinco primeiros termos da sequência. Perceba que
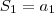
,

,

, e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
Mas eu não tenho o valor de nehum termo então como au encontro o resultado?
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Qua Nov 30, 2011 21:46
por MarceloFantini » Qua Nov 30, 2011 21:46
O enunciado parece ter dito que o valor da soma de N termos é

, use isso juntamente com o que eu disse.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matem » Qua Nov 30, 2011 21:51
por matem » Qua Nov 30, 2011 21:51
MarceloFantini escreveu:O enunciado parece ter dito que o valor da soma de N termos é

, use isso juntamente com o que eu disse.
Desculpe mas eu não estou entendendo , quando o professor passou o conteudo eu estava internada no hospital , então ele me explicou por cima e estou procurando em livros mas está dificil, desculpa por estar incomodando.
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Qua Nov 30, 2011 22:13
por MarceloFantini » Qua Nov 30, 2011 22:13
A soma de um único termo é o próprio primeiro termo, logo
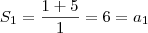
.
A soma dos dois primeiros termos é

, logo
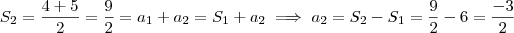
.
A soma dos três primeiros termos é
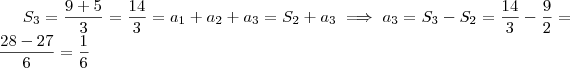
.
A soma dos quatro primeiros termos é
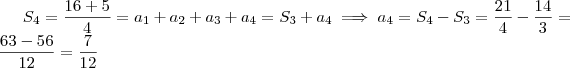
.
Note que tudo isto depende se a minha interpretação do enunciado estiver correta, pois você disse:
por favor me ajudem na sequencia definida por an=n²+5 dividido por n, escrver os 5 primeiros termos da pa.
Se ele te dá o termo geral, basta substituir N pelo termo que você quer, por exemplo n = 2 significa o segundo termo, porém note que este não é o termo geral de uma progressão aritmética, portanto eu deduzi que o enunciado na verdade queira dizer que dada a
soma da sequência definida pela relação, escrever os 5 primeiros termos da
sequência, que não é
necessariamente uma P.A.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6136 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4727 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5630 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4426 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8402 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , isto é, a soma de n+1 termos menos a soma de n termos.
, isto é, a soma de n+1 termos menos a soma de n termos.

, isto é, a soma de n+1 termos menos a soma de n termos.

 . Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de
. Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de  , sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos
, sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos  encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo
encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo  .
.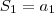 ,
,  ,
,  , e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
, e assim em diante. Usando o método que expliquei acima, você chegará na resposta.

 . Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de
. Você não sabe o valor deles individualmente, mas você sabe a soma. Agora, você quer descobrir o valor de  , sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos
, sendo que você sabe calcular a soma para qualquer quantidade de termos. Ora, se fizermos  encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo
encontraremos o desejado, mas isso é simplesmente fazer a soma dos cinco termos menos a soma dos quatro termos, logo  .
.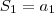 ,
,  ,
,  , e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
, e assim em diante. Usando o método que expliquei acima, você chegará na resposta.
 , use isso juntamente com o que eu disse.
, use isso juntamente com o que eu disse.

, use isso juntamente com o que eu disse.

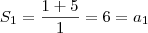 .
.  , logo
, logo 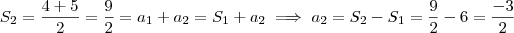 .
. 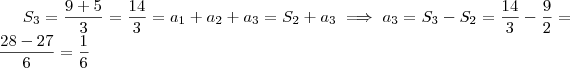 .
. 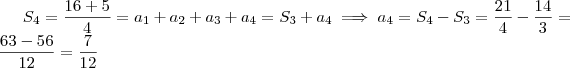 .
.
