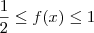Para que uma função seja periódica, deve ser válida a seguinte igualdade:
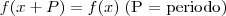
Temos, portanto, que tentar expressar a função desejada do modo acima. Começaremos organizando-a de outro modo:
![f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore](/latexrender/pictures/8369cc957a4a379a926adfa8ad9a81fd.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/67934cfc9b0bbec125b94f767a014717.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/14148f48f94826039e9a56c7ce51745d.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1} \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1}](/latexrender/pictures/69cdded71ee4f383679fef1089e80d0e.png)
Para facilitar, vamos fazer a seguinte substituição:
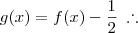
![\left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2 \left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2](/latexrender/pictures/5bc54eb052657fe457d327269dd512f7.png)
Se agora considerarmos a função para
x = x + a, teremos:
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore](/latexrender/pictures/d7a0bf58ea4ccbea0cc42e1cc289aa0d.png)
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/258ee2672309e983bba4e4d8bc92be20.png)
![\left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/3d8cabb06d1504c04b8d98621185d0ed.png)

Para justificar o último passo, note (através de
1) que:
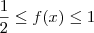
Consequentemente:

Isso é o bastante para justificar que
g(x+2a) = g(x). Como
g(x) = f(x) - 1/2 , analisando graficamente, notamos que o termo
-1/2 só desloca o gráfico de
f(x) sem alterar sua forma, tampouco sua periodicidade. Demonstramos então que
f(x) é uma função periódica cujo período é
2a.
 a
a 

![f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}} f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}}](/latexrender/pictures/ea892c68adbdd818a1fec22c9e3b64cf.png) , f é periódica?
, f é periódica?
 a
a 

![f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}} f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}}](/latexrender/pictures/ea892c68adbdd818a1fec22c9e3b64cf.png) , f é periódica?
, f é periódica?
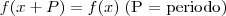
![f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore](/latexrender/pictures/8369cc957a4a379a926adfa8ad9a81fd.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/67934cfc9b0bbec125b94f767a014717.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/14148f48f94826039e9a56c7ce51745d.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1} \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1}](/latexrender/pictures/69cdded71ee4f383679fef1089e80d0e.png)
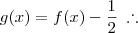
![\left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2 \left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2](/latexrender/pictures/5bc54eb052657fe457d327269dd512f7.png)
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore](/latexrender/pictures/d7a0bf58ea4ccbea0cc42e1cc289aa0d.png)
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/258ee2672309e983bba4e4d8bc92be20.png)
![\left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/3d8cabb06d1504c04b8d98621185d0ed.png)