 por rochadapesada » Sáb Dez 14, 2013 21:29
por rochadapesada » Sáb Dez 14, 2013 21:29
a letra "a", eu respondi que, como ele forma um tetraedro, eles (os vetores) tem que ser LI e portanto formam uma base (Não sei se estou certo)
a "b" não conseguir desenvolver
- Anexos
-

-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Sáb Dez 14, 2013 23:54
por Russman » Sáb Dez 14, 2013 23:54
Sim. Um conjunto de vetores é base de um espaço se, e somente se, este conjunto é LI e GERA o espaço. Isto é, os vetores desse espaço se escrevem de FORMA ÚNICA como combinação linear dos vetores da base.
Exemplo: Por que que
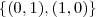
gera o

?
Gera poque o conjunto é LI( a solução
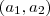
de
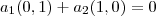
é apenas
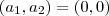
) e existe apenas um par de números reais
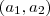
tais que um vetor

pertença a

. É fácil de mostrar. Suponha que
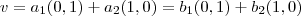
. Assim,
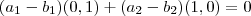
Mas, como o conjunto é LI a única solução possível dessa equação é
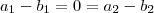
de modo que
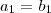
e
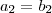
. Portanto, o vetor se escreve de forma única.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por rochadapesada » Dom Dez 15, 2013 00:20
por rochadapesada » Dom Dez 15, 2013 00:20
Estou dando geometria analítica, não cheguei em álgebra linear ainda :/ ... Ai essa questão é para responder com geometria analítica
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Dom Dez 15, 2013 00:28
por Russman » Dom Dez 15, 2013 00:28
Qual a definição de base que te apresentaram?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por rochadapesada » Dom Dez 15, 2013 00:37
por rochadapesada » Dom Dez 15, 2013 00:37
O básico que 3 vetores tem que ser LI, que a norma de u é a raiz de a1^2+a2^2+a3^2 apenas isso... peguei do livro tratamento vetorial...
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Dom Dez 15, 2013 02:42
por Russman » Dom Dez 15, 2013 02:42
Isso não é suficiente e nem necessário pra definir base.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Dom Dez 15, 2013 11:03
por e8group » Dom Dez 15, 2013 11:03
Define-se Base na álgebra linear( vide livro
http://toandaihoc.files.wordpress.com/2 ... lgebra.pdf página 41 ) da seguinte forma :
" Definition. Let V be a vector space. A basis for V is a linearly inde
pendent set of vectors in V which spans the space V. The space V is finite
dimensional if it has a fim:te basis."
Entretanto há um resultado A.L. que diz se

é um espaço vetorial de dimensão finita,digamos

,então qualquer subconjunto de

linearmente independente cuja cardinalidade é

constitui-se uma base para

.
Como em G.A. em geral trabalhamos no

( máximo n = 3) ,

é um espaço vetorial de dimensão finita que és

.Desta forma podemos definir base utilizando o resultado acima . De acordo com o livro de G.A . o qual já mencionei , lá defini-se base p/ V^3 como tripla ordenada

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Dom Dez 15, 2013 14:18
por Russman » Dom Dez 15, 2013 14:18
santhiago escreveu:" Definition. Let V be a vector space. A basis for V is a linearly inde
pendent set of vectors in V which spans the space V. The space V is finite
dimensional if it has a fim:te basis."
Entretanto há um resultado A.L. que diz se é um espaço vetorial de dimensão finita,digamos ,então qualquer subconjunto de linearmente independente cuja cardinalidade é constitui-se uma base para .
espaço
Perfeito. A base é um conjunto LI que gera o espaço. Veja que se o conjunto é LI e subconjunto do espaço então este pode ser uma base.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Vértices do tetraedro
por -civil- » Qua Ago 17, 2011 22:38
- 1 Respostas
- 2575 Exibições
- Última mensagem por LuizAquino

Qua Ago 17, 2011 23:17
Geometria Analítica
-
- Vértices do tetraedro e equação geral do plano
por -civil- » Qua Jun 15, 2011 23:04
- 1 Respostas
- 4015 Exibições
- Última mensagem por LuizAquino

Qui Jun 16, 2011 17:57
Geometria Analítica
-
- [Produto Escalar] Coordenadas em base ortonormal
por LucasSG » Qua Mai 29, 2013 17:47
- 3 Respostas
- 2052 Exibições
- Última mensagem por temujin

Qui Mai 30, 2013 23:12
Geometria Analítica
-
- [os afixos formam qual polígono?]
por JKS » Qui Jun 20, 2013 01:38
- 0 Respostas
- 957 Exibições
- Última mensagem por JKS

Qui Jun 20, 2013 01:38
Números Complexos
-
- [Lógica Digital] Sistema Numérico Conversão Base X - Base 10
por Luc4sPaulo » Sex Fev 17, 2017 12:32
- 0 Respostas
- 4158 Exibições
- Última mensagem por Luc4sPaulo

Sex Fev 17, 2017 12:32
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



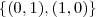 gera o
gera o  ?
?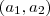 de
de 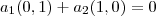 é apenas
é apenas 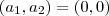 ) e existe apenas um par de números reais
) e existe apenas um par de números reais 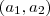 tais que um vetor
tais que um vetor  pertença a
pertença a  . É fácil de mostrar. Suponha que
. É fácil de mostrar. Suponha que 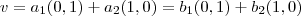 . Assim,
. Assim,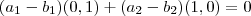
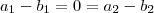 de modo que
de modo que 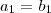 e
e 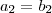 . Portanto, o vetor se escreve de forma única.
. Portanto, o vetor se escreve de forma única.




 é um espaço vetorial de dimensão finita,digamos
é um espaço vetorial de dimensão finita,digamos  ,então qualquer subconjunto de
,então qualquer subconjunto de  linearmente independente cuja cardinalidade é
linearmente independente cuja cardinalidade é  constitui-se uma base para
constitui-se uma base para  .
. ( máximo n = 3) ,
( máximo n = 3) ,  é um espaço vetorial de dimensão finita que és
é um espaço vetorial de dimensão finita que és  .Desta forma podemos definir base utilizando o resultado acima . De acordo com o livro de G.A . o qual já mencionei , lá defini-se base p/ V^3 como tripla ordenada
.Desta forma podemos definir base utilizando o resultado acima . De acordo com o livro de G.A . o qual já mencionei , lá defini-se base p/ V^3 como tripla ordenada  .
.






