 por jordyson rocha » Qua Jan 30, 2013 12:17
por jordyson rocha » Qua Jan 30, 2013 12:17
Considerando-se que o afixo do número complexo z = a + bi é ponto da reta y = 5x, pode-se afirmar
que o afixo do número complexo ? iz é ponto da reta
01) y ? x = 0.
02) y ? 3x = 0.
03) y + 5x = 0.
04) y - x/5 = 0 .
05) y + x/5 = 0.
Olha eu não entendi como eu uso a função, de primeiro grau, na questão e nem pq o "y" não tem coeficiente. muito obrigado pela resposta
-
jordyson rocha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Jan 30, 2013 11:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qua Jan 30, 2013 17:31
por young_jedi » Qua Jan 30, 2013 17:31
se o afixo é dado pela função então z sera
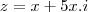
e
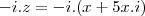

tente concluir e comente as duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por jordyson rocha » Qua Jan 30, 2013 18:13
por jordyson rocha » Qua Jan 30, 2013 18:13
olha não entendo uma coisa...A reta segue a função y = ax + b só que o "b" vale 0 e isso eu não consigo aplicar na questão.Não estou conseguindo terminar. Em nenhum lugar eu to vendo algo parecido com isso!
-
jordyson rocha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Jan 30, 2013 11:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Jan 30, 2013 18:26
por Russman » Qua Jan 30, 2013 18:26
o afixo de um número complexo
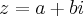
é o ponto de coordenadas

no plano de Argand-Gauss.
Assim, o valor

representa uma coordenada

e o valor

uma

.
Se

, isto é, se

é função de

e , no caso,
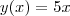
, então todos os complexos que estão sobre esta reta( que são pontos dessa reta) são da forma
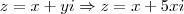
.
Agora, o número complexo

é da forma
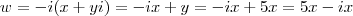
.
Ou seja,

de forma que

é a reta do que contem os afixos de
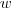
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qua Jan 30, 2013 18:33
por Russman » Qua Jan 30, 2013 18:33
jordyson rocha escreveu:olha não entendo uma coisa...A reta segue a função y = ax + b só que o "b" vale 0 e isso eu não consigo aplicar na questão.Não estou conseguindo terminar. Em nenhum lugar eu to vendo algo parecido com isso!
Não! O número complexo é da forma
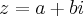
onde esses valores a e b da forma

podem representar um ponto em um plano. E disto podemos imaginar uma função a qual esse ponto pertença. Essa é a ideia.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jordyson rocha » Qui Jan 31, 2013 17:57
por jordyson rocha » Qui Jan 31, 2013 17:57
Cara muito obrigado vlw msm, essa questão vai me ajudar bastante no entendimento de outras.
-
jordyson rocha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Jan 30, 2013 11:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17104 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13316 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10317 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
-
- Números Complexos
por Cleyson007 » Qui Mai 14, 2009 13:57
- 7 Respostas
- 13931 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 11:04
Números Complexos
-
- NUMEROS COMPLEXOS
por lieberth » Sáb Jun 13, 2009 13:48
- 1 Respostas
- 4100 Exibições
- Última mensagem por Marcampucio

Sáb Jun 13, 2009 14:35
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


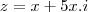
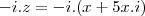


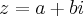 é o ponto de coordenadas
é o ponto de coordenadas  no plano de Argand-Gauss.
no plano de Argand-Gauss. representa uma coordenada
representa uma coordenada  e o valor
e o valor  uma
uma  .
. , isto é, se
, isto é, se 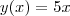 , então todos os complexos que estão sobre esta reta( que são pontos dessa reta) são da forma
, então todos os complexos que estão sobre esta reta( que são pontos dessa reta) são da forma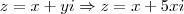 .
. é da forma
é da forma 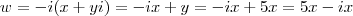 .
. de forma que
de forma que  é a reta do que contem os afixos de
é a reta do que contem os afixos de  .
. .
. ,
,  e para
e para  ,
,  .
.
 .
.
