[Equação de planos] Dúvida exercício 5

por **MrJuniorFerr** » Qui Out 11, 2012 08:58

Olá pessoal, estou com dúvida no seguinte exercício:

Escreva as equações paramétricas da interseção dos planos $\pi1: 2x+y-z=0$ e $\pi2: x+y+z=1$

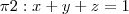
O primeiro passo é encontrar a interseção dos dois planos dados, ou seja, encontrar uma reta. Fiz isto, encontrei o ponto $I(x,\frac{-3x}{2},\frac{1x}{2})$ . Desde então, atribui x=1

e

e achei os pontos $A(1,\frac{-3}{2},\frac{1}{2})$ e B(2,-3,1)

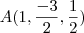respectivamente. Fazendo $\overrightarrow{AB}=(1,\frac{-3}{2},\frac{1}{2})$ , encontrei o vetor diretor dessa reta. Portanto, como podem ver, tenho 2 pontos e o vetor diretor da reta, ou seja, tenho a reta.
Mas, eis a questão... o que fazer agora? Tenho somente os dados de uma reta. Como achar as equações paramétricas do plano?

por **MarceloFantini** » Qui Out 11, 2012 11:03

O resultado é uma reta. A interseção de dois planos será um plano se e somente se eles coincidirem.

por **MrJuniorFerr** » Qui Out 11, 2012 11:30

MarceloFantini escreveu:O resultado é uma reta. A interseção de dois planos será um plano se e somente se eles coincidirem.

Entendi Marcelo. Portanto, é só eu passar os dados da reta que obtive para uma equação paramétrica da reta e esta mesma será a equação paramétrica do plano.
Obrigado

por **MarceloFantini** » Qui Out 11, 2012 11:37

Será equação paramétrica de uma reta, que será a equação paramétrica da interseção dos planos.

por **MrJuniorFerr** » Qui Out 11, 2012 12:43

MarceloFantini escreveu:Será equação paramétrica de uma reta, que será a equação paramétrica da interseção dos planos.

Foi uma falha na minha interpretação...
Independentemente se a interseção dos dois planos forem uma reta ou um plano, a equação paramétrica será o obtido a partir desta interseção.

[Equação de planos] Dúvida exercício 5

[Equação de planos] Dúvida exercício 5

[Equação de planos] Dúvida exercício 5

Re: [Equação de planos] Dúvida exercício 5

Re: [Equação de planos] Dúvida exercício 5

Re: [Equação de planos] Dúvida exercício 5

Re: [Equação de planos] Dúvida exercício 5

Quem está online