Escreva as equações paramétricas da interseção dos planos
 e
e 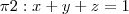
O primeiro passo é encontrar a interseção dos dois planos dados, ou seja, encontrar uma reta. Fiz isto, encontrei o ponto
 . Desde então, atribui
. Desde então, atribui  e
e  e achei os pontos
e achei os pontos 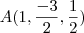 e
e  respectivamente. Fazendo
respectivamente. Fazendo  , encontrei o vetor diretor dessa reta. Portanto, como podem ver, tenho 2 pontos e o vetor diretor da reta, ou seja, tenho a reta.
, encontrei o vetor diretor dessa reta. Portanto, como podem ver, tenho 2 pontos e o vetor diretor da reta, ou seja, tenho a reta.Mas, eis a questão... o que fazer agora? Tenho somente os dados de uma reta. Como achar as equações paramétricas do plano?





 .
.



