 por MrJuniorFerr » Qui Out 11, 2012 08:58
por MrJuniorFerr » Qui Out 11, 2012 08:58
Olá pessoal, estou com dúvida no seguinte exercício:
Escreva as equações paramétricas da interseção dos planos  e
e 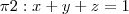
O primeiro passo é encontrar a interseção dos dois planos dados, ou seja, encontrar uma reta. Fiz isto, encontrei o ponto

. Desde então, atribui

e

e achei os pontos
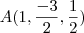
e

respectivamente. Fazendo

, encontrei o vetor diretor dessa reta. Portanto, como podem ver, tenho 2 pontos e o vetor diretor da reta, ou seja, tenho a reta.
Mas, eis a questão... o que fazer agora? Tenho somente os dados de uma reta. Como achar as equações paramétricas do plano?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Qui Out 11, 2012 11:03
por MarceloFantini » Qui Out 11, 2012 11:03
O resultado é uma reta. A interseção de dois planos será um plano se e somente se eles coincidirem.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Qui Out 11, 2012 11:30
por MrJuniorFerr » Qui Out 11, 2012 11:30
MarceloFantini escreveu:O resultado é uma reta. A interseção de dois planos será um plano se e somente se eles coincidirem.
Entendi Marcelo. Portanto, é só eu passar os dados da reta que obtive para uma equação paramétrica da reta e esta mesma será a equação paramétrica do plano.
Obrigado
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Qui Out 11, 2012 11:37
por MarceloFantini » Qui Out 11, 2012 11:37
Será equação paramétrica de uma reta, que será a equação paramétrica da interseção dos planos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Qui Out 11, 2012 12:43
por MrJuniorFerr » Qui Out 11, 2012 12:43
MarceloFantini escreveu:Será equação paramétrica de uma reta, que será a equação paramétrica da interseção dos planos.
Foi uma falha na minha interpretação...
Independentemente se a interseção dos dois planos forem uma reta ou um plano, a equação paramétrica será o obtido a partir desta interseção.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação de planos] Dúvida exercício
por MrJuniorFerr » Sáb Out 06, 2012 17:16
- 2 Respostas
- 3948 Exibições
- Última mensagem por MrJuniorFerr

Sáb Out 06, 2012 18:19
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 2
por MrJuniorFerr » Sáb Out 06, 2012 20:39
- 14 Respostas
- 9058 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 19:07
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 3
por MrJuniorFerr » Dom Out 07, 2012 02:49
- 3 Respostas
- 2329 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 17:21
Geometria Analítica
-
- [Equação de planos] Dúvida exercício 4
por MrJuniorFerr » Seg Out 08, 2012 07:40
- 1 Respostas
- 1334 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 10:06
Geometria Analítica
-
- [Equação de planos] Dúvida exercício 6
por MrJuniorFerr » Qui Out 11, 2012 20:43
- 8 Respostas
- 3563 Exibições
- Última mensagem por MrJuniorFerr

Qui Out 11, 2012 21:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e 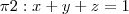
 . Desde então, atribui
. Desde então, atribui  e
e  e achei os pontos
e achei os pontos 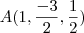 e
e  respectivamente. Fazendo
respectivamente. Fazendo  , encontrei o vetor diretor dessa reta. Portanto, como podem ver, tenho 2 pontos e o vetor diretor da reta, ou seja, tenho a reta.
, encontrei o vetor diretor dessa reta. Portanto, como podem ver, tenho 2 pontos e o vetor diretor da reta, ou seja, tenho a reta.



