 por Claudin » Ter Ago 02, 2011 02:42
por Claudin » Ter Ago 02, 2011 02:42
Não consigo resolver este exercício de limite de função composta.
![\lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}} \lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}](/latexrender/pictures/cc40839f72d2793dffb732bc7d90e2ec.png)
Desculpe, coloquei um valor equivocado
a verdadeira expressão seria esta aqui em cima.
Obrigado
Editado pela última vez por
Claudin em Ter Ago 02, 2011 15:50, em um total de 1 vez.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Ter Ago 02, 2011 09:25
por FilipeCaceres » Ter Ago 02, 2011 09:25
Olá Claudin,
Teste fazer usando o mesmo que foi feito
aquiAbraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Ter Ago 02, 2011 16:09
por Claudin » Ter Ago 02, 2011 16:09
Já tentei de várias formas mas não consigo!
Tenho que começar assim?
![\lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}\Rightarrow\sqrt[3]{u} \lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}\Rightarrow\sqrt[3]{u}](/latexrender/pictures/1d6fc384bba699065097db3afcad1f9f.png)
onde

e
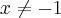
Mas não consigo a resposta correta!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Ter Ago 02, 2011 16:46
por FilipeCaceres » Ter Ago 02, 2011 16:46
Olá Claudin,
Para está questão basta fazer o seguinte,
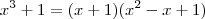
Logo,
![\lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}=\lim_{x\rightarrow-1}\sqrt[3]{\frac{\cancel{(x+1)}(x^2-x+1)}{\cancel{(x+1)}}} \lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}=\lim_{x\rightarrow-1}\sqrt[3]{\frac{\cancel{(x+1)}(x^2-x+1)}{\cancel{(x+1)}}}](/latexrender/pictures/a1afda6e5652c34b733c478de353aa23.png)
, pois
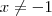
.
Assim temos,
![\lim_{x\rightarrow-1}\sqrt[3]{x^2-x+1}=\sqrt[3]{(-1)^2+1+1}=\boxed{\sqrt[3]{3}} \lim_{x\rightarrow-1}\sqrt[3]{x^2-x+1}=\sqrt[3]{(-1)^2+1+1}=\boxed{\sqrt[3]{3}}](/latexrender/pictures/b6d2a507951a87622cfc7acfa9628ad4.png)
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Ter Ago 02, 2011 17:25
por Claudin » Ter Ago 02, 2011 17:25
Obrigado

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6642 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4787 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5118 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7257 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4434 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}} \lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}](/latexrender/pictures/cc40839f72d2793dffb732bc7d90e2ec.png)

![\lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}} \lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}](/latexrender/pictures/cc40839f72d2793dffb732bc7d90e2ec.png)


![\lim_{x\rightarrow-1}\frac{\sqrt[3]{{x}^{3}+1}}{x+1} \lim_{x\rightarrow-1}\frac{\sqrt[3]{{x}^{3}+1}}{x+1}](/latexrender/pictures/66dbb2e9c5a6b3bc338edf491b9e39d2.png)
![\lim_{x\rightarrow-1}\frac{\sqrt[3]{(x+1)({x}^{2}-x+1)}}{x+1} \lim_{x\rightarrow-1}\frac{\sqrt[3]{(x+1)({x}^{2}-x+1)}}{x+1}](/latexrender/pictures/befbe1e291fd8744bc88f82ddd2244f0.png)
![\lim_{x\rightarrow-1}\frac{\sqrt[3]{({x}^{2}-x+1)}}{{x+1}^{\frac{2}{3}}} \lim_{x\rightarrow-1}\frac{\sqrt[3]{({x}^{2}-x+1)}}{{x+1}^{\frac{2}{3}}}](/latexrender/pictures/65866f2613ae5a6bc34c194714135b38.png)
![\lim_{x\rightarrow-1}\frac{\sqrt[3]{3}}{0} \lim_{x\rightarrow-1}\frac{\sqrt[3]{3}}{0}](/latexrender/pictures/8546f5d781f8b49f0b4617b2c67fd00b.png)
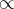

![\lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}\Rightarrow\sqrt[3]{u} \lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}\Rightarrow\sqrt[3]{u}](/latexrender/pictures/1d6fc384bba699065097db3afcad1f9f.png) onde
onde  e
e 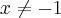

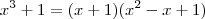
![\lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}=\lim_{x\rightarrow-1}\sqrt[3]{\frac{\cancel{(x+1)}(x^2-x+1)}{\cancel{(x+1)}}} \lim_{x\rightarrow-1}\sqrt[3]{\frac{x^3+1}{x+1}}=\lim_{x\rightarrow-1}\sqrt[3]{\frac{\cancel{(x+1)}(x^2-x+1)}{\cancel{(x+1)}}}](/latexrender/pictures/a1afda6e5652c34b733c478de353aa23.png) , pois
, pois 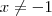 .
.![\lim_{x\rightarrow-1}\sqrt[3]{x^2-x+1}=\sqrt[3]{(-1)^2+1+1}=\boxed{\sqrt[3]{3}} \lim_{x\rightarrow-1}\sqrt[3]{x^2-x+1}=\sqrt[3]{(-1)^2+1+1}=\boxed{\sqrt[3]{3}}](/latexrender/pictures/b6d2a507951a87622cfc7acfa9628ad4.png)



 .
.



