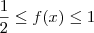Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Balanar » Sáb Ago 07, 2010 17:58
por Balanar » Sáb Ago 07, 2010 17:58
IME-96
Seja f uma função real tal que

a


![f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}} f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}}](/latexrender/pictures/ea892c68adbdd818a1fec22c9e3b64cf.png)
, f é periódica?
Justifique:
Resposta:
f é periódica de período 2a.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Sáb Ago 28, 2010 17:02
por Douglasm » Sáb Ago 28, 2010 17:02
Para que uma função seja periódica, deve ser válida a seguinte igualdade:
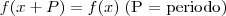
Temos, portanto, que tentar expressar a função desejada do modo acima. Começaremos organizando-a de outro modo:
![f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore](/latexrender/pictures/8369cc957a4a379a926adfa8ad9a81fd.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/67934cfc9b0bbec125b94f767a014717.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/14148f48f94826039e9a56c7ce51745d.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1} \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1}](/latexrender/pictures/69cdded71ee4f383679fef1089e80d0e.png)
Para facilitar, vamos fazer a seguinte substituição:
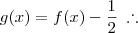
![\left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2 \left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2](/latexrender/pictures/5bc54eb052657fe457d327269dd512f7.png)
Se agora considerarmos a função para
x = x + a, teremos:
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore](/latexrender/pictures/d7a0bf58ea4ccbea0cc42e1cc289aa0d.png)
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/258ee2672309e983bba4e4d8bc92be20.png)
![\left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/3d8cabb06d1504c04b8d98621185d0ed.png)

Para justificar o último passo, note (através de
1) que:
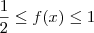
Consequentemente:

Isso é o bastante para justificar que
g(x+2a) = g(x). Como
g(x) = f(x) - 1/2 , analisando graficamente, notamos que o termo
-1/2 só desloca o gráfico de
f(x) sem alterar sua forma, tampouco sua periodicidade. Demonstramos então que
f(x) é uma função periódica cujo período é
2a.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Balanar » Sáb Ago 28, 2010 17:50
por Balanar » Sáb Ago 28, 2010 17:50
Brilhante resposta, parabéns.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Sáb Ago 28, 2010 17:59
por Douglasm » Sáb Ago 28, 2010 17:59
Que nada, eu já conhecia esse tipo de questão. =)
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por kamillanjb » Ter Mar 15, 2011 22:57
por kamillanjb » Ter Mar 15, 2011 22:57
MAs tá muito bem explicado. Sério mesmo. De grande ajuda.
-
kamillanjb
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Fev 16, 2011 10:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.G. Dízima Periódica
por Rafael16 » Qua Jul 18, 2012 19:48
- 3 Respostas
- 8152 Exibições
- Última mensagem por Russman

Qua Jul 18, 2012 21:20
Progressões
-
- Dizima periodica composta
por creberson » Sex Mai 24, 2019 11:03
- 1 Respostas
- 9627 Exibições
- Última mensagem por DanielFerreira

Qui Set 12, 2019 23:19
Conjuntos
-
- [Sequência convergente e periódica ] Prove ...
por e8group » Seg Jan 20, 2014 23:45
- 0 Respostas
- 8447 Exibições
- Última mensagem por e8group

Seg Jan 20, 2014 23:45
Sequências
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5562 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4587 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 a
a 

![f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}} f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}}](/latexrender/pictures/ea892c68adbdd818a1fec22c9e3b64cf.png) , f é periódica?
, f é periódica?
 a
a 

![f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}} f(x+a)=\frac{1}{2}+\sqrt[]{f(x)-{\left[ f(x) \right]}^{2}}}](/latexrender/pictures/ea892c68adbdd818a1fec22c9e3b64cf.png) , f é periódica?
, f é periódica?
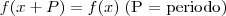
![f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore f(x+a) = \frac{1}{2} + \sqrt{f(x) - [f(x)]^2} \;\therefore](/latexrender/pictures/8369cc957a4a379a926adfa8ad9a81fd.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/67934cfc9b0bbec125b94f767a014717.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \frac{1}{4} + f(x) - [f(x)]^2 \;\therefore](/latexrender/pictures/14148f48f94826039e9a56c7ce51745d.png)
![\left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1} \left[f(x+a) - \frac{1}{2}\right]^2 = \frac{1}{4} - \left[f(x) - \frac{1}{2}\right]^2 \;\fbox{1}](/latexrender/pictures/69cdded71ee4f383679fef1089e80d0e.png)
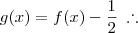
![\left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2 \left[g(x+a)\right]^2 = \frac{1}{4} - \left[g(x)\right]^2](/latexrender/pictures/5bc54eb052657fe457d327269dd512f7.png)
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \left[g(x + a)\right]^2 \;\therefore](/latexrender/pictures/d7a0bf58ea4ccbea0cc42e1cc289aa0d.png)
![\left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \frac{1}{4} - \frac{1}{4} + \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/258ee2672309e983bba4e4d8bc92be20.png)
![\left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore \left[g(x+2a)\right]^2 = \left[g(x)\right]^2 \;\therefore](/latexrender/pictures/3d8cabb06d1504c04b8d98621185d0ed.png)