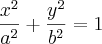por TheoFerraz » Seg Nov 07, 2011 15:10
por TheoFerraz » Seg Nov 07, 2011 15:10
Lembre-se, o domínio da função se refere ao x e ao y em absoluto.
é interessante pensar assim, "quais valores de x ou de y eu posso ou não posso colocar aqui ?"
no caso, voce pode colocar absolutamente qualquer valor real... em x e em y. não tem nenhuma restrição!
Se a sua função envolvesse uma raiz quadrada, ou um logarítimo, ou funcões nas quais não faz sentido calcular num conjuntos de números ai voce veria qual faz e qual nao faz sentido calcular, todos os que fizerem sentido calcular na função pertencem ao domínio!
se voce estiver falando da imagem é outra coisa (com voce está estudando funções de 2 variáveis acredito que voce pode ter confundido com a imagem)
se for o caso voce deve igualar a função a um numero

e ver quais numeros

podem ser atingidos pela função.
Explicitando a imagem:


do lado direito da igualdade só é possível obter numeros maiores do que zero.... o segundo lado da igualdade tem que obedecer o mesmo:
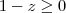

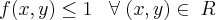
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 15:49
por TheoFerraz » Seg Nov 07, 2011 15:49
Isso que voce falou é BEM arriscado... existem plinomios de segundo grau.. ou terceiro. em fim, que tem parte imaginária! ou por exemplo voce nunca pode dividir por zero... todas essas coiass voce vai usar pra determinar o domínio...
Vamos às funçoes:
a primeira delas o domínio é real. QUALQUER valor de x e y que voce usar, voce consegue um resultado real, (obs, diz-se que o domínio é

pois estamos falando de duas variáveis...)
a segunda é mais complicada... voce sabe que existem duas condições... não se pode dividir por zero, e a raiz nunca pode ser avaliada em numeros negativos (no caso real)
entao as condiçoes de existencia são:
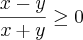
e

quanto à primeira condição, temos:
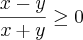
isso é complicado... devemos fazer um estudo de sinal. o sinal desse resultado depende do sinal do conteúdo de cima e do de baixo! vamos chamar essa inequação de (A)
(A) terá resultado positivo se e somente se, os resultados "de cima" e "de baixo" da fração, resultarem no mesmo sinal!
desenhe dois planos Oxy e faça sinaizinhos de + na parte que representa o resultado da inequação positivo e a parte que representa o resultado negativo voce faz sinaizinhos de -:
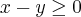
(desenhe a reta y = x. tudo que estiver 'acima' dela é negativo, e abaixo dela é positivo)
faça o mesmo com a parte de baixo da fração:
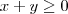
fará parte do domínio da função as areas em que as duas funçoes tiverem sinais iguais!
Lembrando que não se pode dividir por zero entao a outra condição de existencia descrita lá em cima também deve ser levada em conta.
A segunda função voce tenta =)
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por ah001334 » Seg Nov 07, 2011 15:59
por ah001334 » Seg Nov 07, 2011 15:59
oi denovo fiz a segunda equação vê por favor se está certo
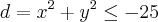
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 16:06
por TheoFerraz » Seg Nov 07, 2011 16:06
quase...
O certo seria maior ou igual.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 16:07
por TheoFerraz » Seg Nov 07, 2011 16:07
opa, pera ai
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 16:08
por TheoFerraz » Seg Nov 07, 2011 16:08
raiz nao pode ser negativa, entao

dai temos que

só isso
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por ah001334 » Seg Nov 07, 2011 16:16
por ah001334 » Seg Nov 07, 2011 16:16
retornando aos seus ensinamentos
então se tenho a função
![z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{} z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{}](/latexrender/pictures/00753fe08d806fd9338e7ab3dedcf8bb.png)
o domínio será
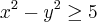
pois não temos raiz negativa?
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por ah001334 » Seg Nov 07, 2011 16:17
por ah001334 » Seg Nov 07, 2011 16:17
opsss 25 no final
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 16:20
por TheoFerraz » Seg Nov 07, 2011 16:20
se não tem raiz negativa, o que está la dentro deve ser maior ou igual a zero.

passando o 25

multiplicando por -1 (e mundando a igualdade)
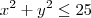
ta ai o domínio
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 16:20
por TheoFerraz » Seg Nov 07, 2011 16:20
aliás... também deve constar no domínio que

-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por ah001334 » Seg Nov 07, 2011 16:31
por ah001334 » Seg Nov 07, 2011 16:31
agora entendi, então sempre que tenho uma raiz positiva devo só alterar os sinais das igualdades?
assim:
![f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4} f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4}](/latexrender/pictures/75bd123e1e739912b46befd0bd4db182.png)
será


-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 16:39
por TheoFerraz » Seg Nov 07, 2011 16:39
Vamos com muita calma.
O negocio é o seguinte... o que vai dentro da raiz TEM que ser maior ou igual a zero.
Tudo bem... isso é facil...
a questão que eu to aplicando sempre uma propriedade que parece que voce não sabe/lembra
na teoria de equações, o que eu faço quando eu tenho

e eu quero explicitar x?
eu multiplico por -1 em ambos os lados. fica x = 1
em inequações eu posso fazer o mesmo, mas eu tenho que inverter a desigualdade!!!
é só isso, quando voce for passar um numero pro outro lado voce faz igual, quando voce for passar dividindo é igual, em fim. tudo igual. só que pra inverter os sinais voce muda a desigualdade... observe a minha penultima resposta e tente perceber o que eu fiz.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 16:40
por TheoFerraz » Seg Nov 07, 2011 16:40
OBS : sua resposta ao ultimo exercicio estava certinha na penultima passagem...
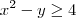
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por ah001334 » Seg Nov 07, 2011 17:02
por ah001334 » Seg Nov 07, 2011 17:02
e para cálculo de curva de nível para essa função

o k vai realizar uma subtração com o 9 do

ou não?
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 17:16
por TheoFerraz » Seg Nov 07, 2011 17:16
não sei bem... a ideia desse "k" não está bem clara pra mim. imagino eu que sejam os níveis!
se for o caso, o que estamos fazendo ? primeiro, intercepte a curva

com o plano

no caso do k = 0
o que obtemos ? quais valores de x e y resolvem a equação
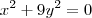
não é dificil perceber que só o par (x,y) = (0,0) resolve isso! observe :
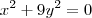

é IMPOSSIVEL algo ao quadrado ser negativo! entao só o que resolve é o zero!
fazendo isso com os outros numeros de k voce vai obtendo curvas implícitas:

vira

para valores de k...
reconhece uma equação de elipse ?
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por ah001334 » Seg Nov 07, 2011 17:39
por ah001334 » Seg Nov 07, 2011 17:39
humm agora me confundi mais ainda!!! pode explicar melhor?
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por TheoFerraz » Seg Nov 07, 2011 18:08
por TheoFerraz » Seg Nov 07, 2011 18:08
curvas de nível são muito simples. mas podem ficar meio chatas se a gente não compreende...
Quando eu tenho uma função
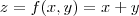
por exemplo. o que significa achar uma curva de nível no nível 0 por exeplo ? cortando isso pelo plano z = 0!
se voce tiver um bom plotador de graficos (caso não tenha
http://math.exeter.edu/rparris/peanut/wppr32z.exe), plote essa curva junto ao plano z = 0... vai ver lá a reta

se eu colocar x + y = 1 por exemplo... é o mesmo. estou interseptando pelo plano z = 1 e vou obter y = 1-x... uma reta também. e assim vai...
No seu caso estamos obtendo equações de elipse! que são da seguinte cara :
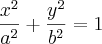
pra mandar bem em curvas de nível tem que saber essas coisas!
parábolas, hiperboles, circunferencias... ou seja, geometria analítica!
no caso do problema anterior para z = 0 eu obtive uma coisa assim

não existe NENHUM x e NENHUM y que resolve isso além do zero para ambos... por que ? x² está igual a um numero negativo!!! (sempre será negativo por que mesmo que o valor de y seja negativo o expoente vai tirar o sinal, mantendo o sinal original) o unico numero que resolve isso é o zero.
quanto ao resto, eu sugiro que voce de uma busca basica em geometria analítica, pode ajudar muito...
outra coisa que pode ajudar é o programa que eu sugeri ai em cima, o winplot. com ele voce plota o grafico e acha as curvas de nível cortando-o por planos z = k
não posso ajudar muuuito mais do que isso... se voce quiser, eu adiciono vc no msn e eu tento te explicar mais calmamente, tudo, passo a passo. mas eu sugiro que voce pegue um bom livro de G.A. e um bom de calculo...
Paulo boulos e James Stewart são otimos...
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por ah001334 » Seg Nov 07, 2011 18:16
por ah001334 » Seg Nov 07, 2011 18:16
vou pegar esses livros hoje na biblioteca, mas o problema é que estudo e não consigo aplicar o conhecimento na resolução dos problemas. Quero aprender e não consigo!!!!
me add se puder me ajuda
semprebela53@hotmail.com
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por procyon » Seg Nov 07, 2011 22:06
por procyon » Seg Nov 07, 2011 22:06
Colega, procure pelo Volume I da coleção "Fundamentos da Matemática Elementar". Toda boa biblioteca possui um.
Estude com muita calma este livro e todos esses seus problemas estarão resolvidos. O livro tem uma bagagem teórica que pode parecer difícil em um primeiro momento mas com o tempo você mais se acostumando e REALMENTE entende porque você não pode fazer isso ou aquilo em uma função.
Dedique o seu tempo livre durante algumas semanas a essa coleção.
Caso já esteja na faculdade, vale a frase "dar um passo atrás para dar dois à frente"
-
procyon
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 31, 2011 23:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dominios e Contradominios
por joaofonseca » Sáb Out 01, 2011 15:09
- 8 Respostas
- 6842 Exibições
- Última mensagem por MarceloFantini

Ter Out 04, 2011 21:19
Funções
-
- calcular domínios de funções
por Regina » Qua Abr 06, 2011 21:17
- 4 Respostas
- 5837 Exibições
- Última mensagem por Regina

Dom Abr 10, 2011 12:38
Funções
-
- Funções Compostas e seus domínios
por NinhaH » Ter Jan 04, 2011 11:58
- 2 Respostas
- 3495 Exibições
- Última mensagem por NinhaH

Qui Jan 06, 2011 11:31
Funções
-
- Leis do Cancelamento em Domínios de Integridade
por m0x0 » Sáb Jul 23, 2011 20:18
- 0 Respostas
- 1842 Exibições
- Última mensagem por m0x0

Sáb Jul 23, 2011 20:18
Álgebra Elementar
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5562 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

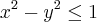


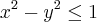

 e ver quais numeros
e ver quais numeros  podem ser atingidos pela função.
podem ser atingidos pela função.


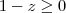

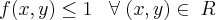

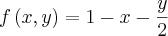
![z= \sqrt[]{\frac{x-y}{x+y}} z= \sqrt[]{\frac{x-y}{x+y}}](/latexrender/pictures/ba3aae9d1cc3593687f25a94e6f918ad.png)
![z=\frac{y}{\sqrt[]{{x}^{2}+{y}^{2}-25}}} z=\frac{y}{\sqrt[]{{x}^{2}+{y}^{2}-25}}}](/latexrender/pictures/fc8349651ebe17214cf9590d0e3d8ad4.png)

 pois estamos falando de duas variáveis...)
pois estamos falando de duas variáveis...)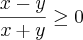

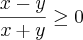
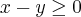
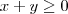

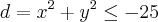






![z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{} z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{}](/latexrender/pictures/00753fe08d806fd9338e7ab3dedcf8bb.png)
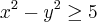




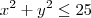



![f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4} f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4}](/latexrender/pictures/75bd123e1e739912b46befd0bd4db182.png)



 e eu quero explicitar x?
e eu quero explicitar x?
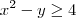


 ou não?
ou não?

 no caso do k = 0
no caso do k = 0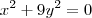
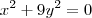





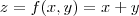 por exemplo. o que significa achar uma curva de nível no nível 0 por exeplo ? cortando isso pelo plano z = 0!
por exemplo. o que significa achar uma curva de nível no nível 0 por exeplo ? cortando isso pelo plano z = 0!