curvas de nível são muito simples. mas podem ficar meio chatas se a gente não compreende...
Quando eu tenho uma função
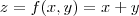
por exemplo. o que significa achar uma curva de nível no nível 0 por exeplo ? cortando isso pelo plano z = 0!
se voce tiver um bom plotador de graficos (caso não tenha
http://math.exeter.edu/rparris/peanut/wppr32z.exe), plote essa curva junto ao plano z = 0... vai ver lá a reta

se eu colocar x + y = 1 por exemplo... é o mesmo. estou interseptando pelo plano z = 1 e vou obter y = 1-x... uma reta também. e assim vai...
No seu caso estamos obtendo equações de elipse! que são da seguinte cara :
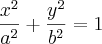
pra mandar bem em curvas de nível tem que saber essas coisas!
parábolas, hiperboles, circunferencias... ou seja, geometria analítica!
no caso do problema anterior para z = 0 eu obtive uma coisa assim

não existe NENHUM x e NENHUM y que resolve isso além do zero para ambos... por que ? x² está igual a um numero negativo!!! (sempre será negativo por que mesmo que o valor de y seja negativo o expoente vai tirar o sinal, mantendo o sinal original) o unico numero que resolve isso é o zero.
quanto ao resto, eu sugiro que voce de uma busca basica em geometria analítica, pode ajudar muito...
outra coisa que pode ajudar é o programa que eu sugeri ai em cima, o winplot. com ele voce plota o grafico e acha as curvas de nível cortando-o por planos z = k
não posso ajudar muuuito mais do que isso... se voce quiser, eu adiciono vc no msn e eu tento te explicar mais calmamente, tudo, passo a passo. mas eu sugiro que voce pegue um bom livro de G.A. e um bom de calculo...
Paulo boulos e James Stewart são otimos...

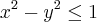


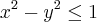

 e ver quais numeros
e ver quais numeros  podem ser atingidos pela função.
podem ser atingidos pela função.


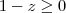

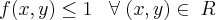

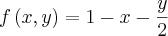
![z= \sqrt[]{\frac{x-y}{x+y}} z= \sqrt[]{\frac{x-y}{x+y}}](/latexrender/pictures/ba3aae9d1cc3593687f25a94e6f918ad.png)
![z=\frac{y}{\sqrt[]{{x}^{2}+{y}^{2}-25}}} z=\frac{y}{\sqrt[]{{x}^{2}+{y}^{2}-25}}}](/latexrender/pictures/fc8349651ebe17214cf9590d0e3d8ad4.png)

 pois estamos falando de duas variáveis...)
pois estamos falando de duas variáveis...)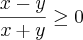

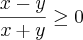
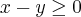
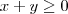

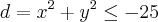






![z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{} z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{}](/latexrender/pictures/00753fe08d806fd9338e7ab3dedcf8bb.png)
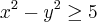




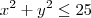



![f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4} f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4}](/latexrender/pictures/75bd123e1e739912b46befd0bd4db182.png)



 e eu quero explicitar x?
e eu quero explicitar x?
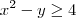


 ou não?
ou não?

 no caso do k = 0
no caso do k = 0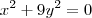
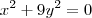





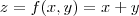 por exemplo. o que significa achar uma curva de nível no nível 0 por exeplo ? cortando isso pelo plano z = 0!
por exemplo. o que significa achar uma curva de nível no nível 0 por exeplo ? cortando isso pelo plano z = 0!
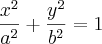






 , avisa que eu resolvo.
, avisa que eu resolvo.

