Olá pessoal, sou novo aqui, estava resolvendo questões de matemática básica mas sou MUITO fraco no assunto, gostaria de pedir a ajuda de vocês. Deixo aqui algumas questões que me deixaram desiludido:
(Tec. Cont.-SC) A caixa de água de uma casa tem capacidade de armazenamento de 2.000 litros. Sabendo que ela possui base quadrada, com 1 metro de lado, assunale a alternativa que indica a altura desta caixa de água.
a) 2 metros (resposta)
b) 20 metros
c) 2 centímetros
d) 2 decímetros
e) 20.000 centímetros
Tentei resolvê-la da seguinte maneira:
se 1litro é igual a 1dm³, e em um quadrado os lados são iguais, então
capacidade = lado1 x lado2 x altura
2000dm³ = 0,1dm x 0,1dm x Altura
Altura = 2000dm³ / 0,01dm²
Altura = 200000dm (ou 20000cm, como na opção do gabarito, mas que não é a certa)
é aqui que eu encalho.. onde eu errei, como chegar em "2m", a resposta da questão, alguem pode me dizer?
(CVM) Um reservatório tem 1,2 m de largura, 1,5 m de comprimento e 1 metro de altura. Para conter 1.260 litros de água, esta deve atingir a altura de:
a) 70 cm (resposta)
b) 0,07 m
c) 7 m
d) 0,7 dm
e) 700 cm
0,12dm x 0,15dm x Altura = 1260dm³
Altura = 1260 / 0,18
Altura = 7000dm (ou 700cm, mas está errado, o gabarito é 70cm)
Quem puder me ajudar, eu agradeço, vlw!


 . Elevando os dois lados ao cubo:
. Elevando os dois lados ao cubo: 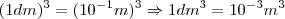 . Como
. Como 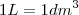 , isso implica que
, isso implica que 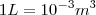 .
.
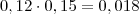 , o que daria 700 dm , consequentemente 70 cm.
, o que daria 700 dm , consequentemente 70 cm.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.