 por natanskt » Seg Out 11, 2010 17:11
por natanskt » Seg Out 11, 2010 17:11
seja S o conjunto de todas as soluções reais da equação
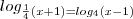 .
. Então:
a-)S é um conjunto e
![s \subset]2,+\infty [ s \subset]2,+\infty [](/latexrender/pictures/26a439b4c6a9fc45588a5af15633d825.png)
b-)S é um conjunto unitário e
![s \subset]1,2[ s \subset]1,2[](/latexrender/pictures/bc8b706c6e5ac5ab24d43832bccf55c3.png)
c-)S possui dois elementos distintos e
![s \subset]-2,2[ s \subset]-2,2[](/latexrender/pictures/270dae8a57ef09443ecf76b09d4d4b6f.png)
d-)S possui dois elementos distintos e
![s \subset]1,+\infty [ s \subset]1,+\infty [](/latexrender/pictures/f24c0d5f3558534e80ebffd0ffdef660.png)
e-)S é o conjunto Vazio
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Seg Out 11, 2010 17:45
por MarceloFantini » Seg Out 11, 2010 17:45
![\log_{\frac{1}{4}} = - \log_4 (x+1) \rightarrow \log_{\frac{1}{4}} (x+1) = - \log_4 (x+1) = \log_4 (x-1) \rightarrow \log_4 (x-1) + \log_4 (x+1) = 0 \rightarrow \log_4 [(x-1)\cdot(x+1)] = 0 \rightarrow 4^0 = (x-1)(x+1) \rightarrow 1 = x^2 -1^2 \rightarrow x^2 = 2 \rightarrow x = \sqrt{2} \log_{\frac{1}{4}} = - \log_4 (x+1) \rightarrow \log_{\frac{1}{4}} (x+1) = - \log_4 (x+1) = \log_4 (x-1) \rightarrow \log_4 (x-1) + \log_4 (x+1) = 0 \rightarrow \log_4 [(x-1)\cdot(x+1)] = 0 \rightarrow 4^0 = (x-1)(x+1) \rightarrow 1 = x^2 -1^2 \rightarrow x^2 = 2 \rightarrow x = \sqrt{2}](/latexrender/pictures/e41153b2ef0b42d4c0fc95847a58baf9.png)
ou

Alternativa A está fora pois a resposta

não está no conjunto dado.
Alternativa B está fora pois
não é um conjunto unitário (são duas respostas).
Alternativa C está dentro pois tem dois elementos distintos e ambos estão no intervalo
![]-2, 2[ ]-2, 2[](/latexrender/pictures/da1d23585b6273019f2e69ed2cd4c39a.png)
.
Alternativa D está fora pelo mesmo motivo da alternativa A.
Alternativa E está fora pois não é vazio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por natanskt » Ter Out 12, 2010 20:06
por natanskt » Ter Out 12, 2010 20:06
fantini aqui no gabarito esta falando que é a ALTERNATIVA B
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Ter Out 12, 2010 20:28
por MarceloFantini » Ter Out 12, 2010 20:28
Natanskt, peço sinceras desculpas. Cometi um erro grotesco. A resposta
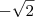
é inválida pois não há como um número positivo ser elevado a um número real e resultar em negativo. A alternativa B está certa mesmo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Ter Out 12, 2010 20:30
por Molina » Ter Out 12, 2010 20:30
Boa noite Fantini e Natan.
Se me permintem, note que

não faz parte da solução, pois caso fizesse o logaritmando do lado direito da igualdade seria negativo, o que contraria a definição de logaritmo.
Assim, a única solução é
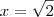
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por natanskt » Qua Out 13, 2010 19:13
por natanskt » Qua Out 13, 2010 19:13
olá,não intendi
essa parte
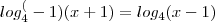
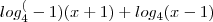
essa parte
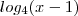
não teria que passar para o outro lado negativo assim -log.......
ou quando é equação logaritmica eu não preciso mudar o sinal
boa noite pessoal
tchau
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Elcioschin » Qua Out 13, 2010 22:55
por Elcioschin » Qua Out 13, 2010 22:55
Natansk
log[1/4](x + 1) = log[4](x - 1) ----> Mudando o primeiro membro para base 4:
log[4](x + 1)/log[4](1/4) = log[4](x - 1) -----> log[4](1/4) = log[4](1) - log[4](4) = 0 - 1 = - 1
- log[4](x + 1) = log[4](x - 1)
log[4](x - 1) + log[4](x + 1) = 0
log[4](x - 1)*(x + 1) = log[4](1)
(x - 1)*(x + 1) = 1
x² - 1 = 1
x² = 2
x = +V2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ITA) equaçoes logaritmica
por natanskt » Qua Out 13, 2010 18:16
- 2 Respostas
- 1366 Exibições
- Última mensagem por MarceloFantini

Sex Out 15, 2010 17:25
Logaritmos
-
- (AMAN) Equaçoes logaritmica
por natanskt » Sex Out 08, 2010 12:37
- 3 Respostas
- 1822 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 16:41
Funções
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3153 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4148 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3427 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
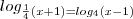 . Então:
. Então:![s \subset]2,+\infty [ s \subset]2,+\infty [](/latexrender/pictures/26a439b4c6a9fc45588a5af15633d825.png)
![s \subset]1,2[ s \subset]1,2[](/latexrender/pictures/bc8b706c6e5ac5ab24d43832bccf55c3.png)
![s \subset]-2,2[ s \subset]-2,2[](/latexrender/pictures/270dae8a57ef09443ecf76b09d4d4b6f.png)
![s \subset]1,+\infty [ s \subset]1,+\infty [](/latexrender/pictures/f24c0d5f3558534e80ebffd0ffdef660.png)

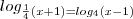 . Então:
. Então:![s \subset]2,+\infty [ s \subset]2,+\infty [](/latexrender/pictures/26a439b4c6a9fc45588a5af15633d825.png)
![s \subset]1,2[ s \subset]1,2[](/latexrender/pictures/bc8b706c6e5ac5ab24d43832bccf55c3.png)
![s \subset]-2,2[ s \subset]-2,2[](/latexrender/pictures/270dae8a57ef09443ecf76b09d4d4b6f.png)
![s \subset]1,+\infty [ s \subset]1,+\infty [](/latexrender/pictures/f24c0d5f3558534e80ebffd0ffdef660.png)

![\log_{\frac{1}{4}} = - \log_4 (x+1) \rightarrow \log_{\frac{1}{4}} (x+1) = - \log_4 (x+1) = \log_4 (x-1) \rightarrow \log_4 (x-1) + \log_4 (x+1) = 0 \rightarrow \log_4 [(x-1)\cdot(x+1)] = 0 \rightarrow 4^0 = (x-1)(x+1) \rightarrow 1 = x^2 -1^2 \rightarrow x^2 = 2 \rightarrow x = \sqrt{2} \log_{\frac{1}{4}} = - \log_4 (x+1) \rightarrow \log_{\frac{1}{4}} (x+1) = - \log_4 (x+1) = \log_4 (x-1) \rightarrow \log_4 (x-1) + \log_4 (x+1) = 0 \rightarrow \log_4 [(x-1)\cdot(x+1)] = 0 \rightarrow 4^0 = (x-1)(x+1) \rightarrow 1 = x^2 -1^2 \rightarrow x^2 = 2 \rightarrow x = \sqrt{2}](/latexrender/pictures/e41153b2ef0b42d4c0fc95847a58baf9.png) ou
ou 
 não está no conjunto dado.
não está no conjunto dado.![]-2, 2[ ]-2, 2[](/latexrender/pictures/da1d23585b6273019f2e69ed2cd4c39a.png) .
.


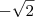 é inválida pois não há como um número positivo ser elevado a um número real e resultar em negativo. A alternativa B está certa mesmo.
é inválida pois não há como um número positivo ser elevado a um número real e resultar em negativo. A alternativa B está certa mesmo.

 não faz parte da solução, pois caso fizesse o logaritmando do lado direito da igualdade seria negativo, o que contraria a definição de logaritmo.
não faz parte da solução, pois caso fizesse o logaritmando do lado direito da igualdade seria negativo, o que contraria a definição de logaritmo.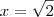

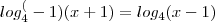
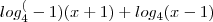 essa parte
essa parte 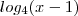 não teria que passar para o outro lado negativo assim -log.......
não teria que passar para o outro lado negativo assim -log.......



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.