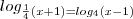 . Então:
. Então:a-)S é um conjunto e
![s \subset]2,+\infty [ s \subset]2,+\infty [](/latexrender/pictures/26a439b4c6a9fc45588a5af15633d825.png)
b-)S é um conjunto unitário e
![s \subset]1,2[ s \subset]1,2[](/latexrender/pictures/bc8b706c6e5ac5ab24d43832bccf55c3.png)
c-)S possui dois elementos distintos e
![s \subset]-2,2[ s \subset]-2,2[](/latexrender/pictures/270dae8a57ef09443ecf76b09d4d4b6f.png)
d-)S possui dois elementos distintos e
![s \subset]1,+\infty [ s \subset]1,+\infty [](/latexrender/pictures/f24c0d5f3558534e80ebffd0ffdef660.png)
e-)S é o conjunto Vazio

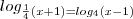 . Então:
. Então:![s \subset]2,+\infty [ s \subset]2,+\infty [](/latexrender/pictures/26a439b4c6a9fc45588a5af15633d825.png)
![s \subset]1,2[ s \subset]1,2[](/latexrender/pictures/bc8b706c6e5ac5ab24d43832bccf55c3.png)
![s \subset]-2,2[ s \subset]-2,2[](/latexrender/pictures/270dae8a57ef09443ecf76b09d4d4b6f.png)
![s \subset]1,+\infty [ s \subset]1,+\infty [](/latexrender/pictures/f24c0d5f3558534e80ebffd0ffdef660.png)

![\log_{\frac{1}{4}} = - \log_4 (x+1) \rightarrow \log_{\frac{1}{4}} (x+1) = - \log_4 (x+1) = \log_4 (x-1) \rightarrow \log_4 (x-1) + \log_4 (x+1) = 0 \rightarrow \log_4 [(x-1)\cdot(x+1)] = 0 \rightarrow 4^0 = (x-1)(x+1) \rightarrow 1 = x^2 -1^2 \rightarrow x^2 = 2 \rightarrow x = \sqrt{2} \log_{\frac{1}{4}} = - \log_4 (x+1) \rightarrow \log_{\frac{1}{4}} (x+1) = - \log_4 (x+1) = \log_4 (x-1) \rightarrow \log_4 (x-1) + \log_4 (x+1) = 0 \rightarrow \log_4 [(x-1)\cdot(x+1)] = 0 \rightarrow 4^0 = (x-1)(x+1) \rightarrow 1 = x^2 -1^2 \rightarrow x^2 = 2 \rightarrow x = \sqrt{2}](/latexrender/pictures/e41153b2ef0b42d4c0fc95847a58baf9.png) ou
ou 
 não está no conjunto dado.
não está no conjunto dado.![]-2, 2[ ]-2, 2[](/latexrender/pictures/da1d23585b6273019f2e69ed2cd4c39a.png) .
.


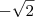 é inválida pois não há como um número positivo ser elevado a um número real e resultar em negativo. A alternativa B está certa mesmo.
é inválida pois não há como um número positivo ser elevado a um número real e resultar em negativo. A alternativa B está certa mesmo.

 não faz parte da solução, pois caso fizesse o logaritmando do lado direito da igualdade seria negativo, o que contraria a definição de logaritmo.
não faz parte da solução, pois caso fizesse o logaritmando do lado direito da igualdade seria negativo, o que contraria a definição de logaritmo.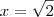

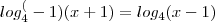
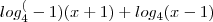 essa parte
essa parte 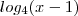 não teria que passar para o outro lado negativo assim -log.......
não teria que passar para o outro lado negativo assim -log.......

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)