



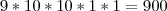






gutorocher escreveu:poderia explicar o que seria os dois últimos uns eu ainda não entendi, poderia explicar de outra forma para ver se consegui compreender....
eu pensei que fosse assim
9 10 10 10 10 e porque é 9 10 10 1 1
poderia esclarecer esta dúvida....



gutorocher escreveu:poderia explicar isso de outra forma ?
Fixando este número, o último algarismo ficará apenas com uma opção (a opção fixada no primeiro dígito):
9 __ __ __ 1
ainda não consigo entender, o porque disso seria uma regra ?


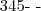 , quais são os dois últimos para que ele seja palíndromo?
, quais são os dois últimos para que ele seja palíndromo?



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.