



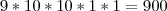






gutorocher escreveu:poderia explicar o que seria os dois últimos uns eu ainda não entendi, poderia explicar de outra forma para ver se consegui compreender....
eu pensei que fosse assim
9 10 10 10 10 e porque é 9 10 10 1 1
poderia esclarecer esta dúvida....



gutorocher escreveu:poderia explicar isso de outra forma ?
Fixando este número, o último algarismo ficará apenas com uma opção (a opção fixada no primeiro dígito):
9 __ __ __ 1
ainda não consigo entender, o porque disso seria uma regra ?


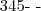 , quais são os dois últimos para que ele seja palíndromo?
, quais são os dois últimos para que ele seja palíndromo?



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)