 por Luanna » Qua Mar 17, 2010 21:29
por Luanna » Qua Mar 17, 2010 21:29
Um cabeleireiro cobra R$ 12,00 pelo corte para clientes com hora marcada e R$ 10,00 para clientes sem hora marcada. Ele atende por dia um número fixo de 6 clientes com hora marcada e um número variável x de clientes sem hora marcada .
a) escreva a fórmula matemática que fornece a quantia Q arrecadada por dia em função do numero x .
b) Qual foi a quantia arrecada num dia em que foram atendidos 16 clientes ?
c) Qual foi o numero de clientes atendidos num dia em que foram arrecadados R$ 212,00 ?
d) Qual é a expressão que indica o numero C de clientes atendidos por dia em função de x ?
-
Luanna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Nov 10, 2009 15:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Elcioschin » Qua Mar 17, 2010 22:07
por Elcioschin » Qua Mar 17, 2010 22:07
a) Q = 12,00*6 + 10,00*x
b) Faça x = 16 acima
c) Faça Q = 212,00 acima
d) C = (x + 6)
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por valeriamsa » Sex Mai 27, 2011 00:23
por valeriamsa » Sex Mai 27, 2011 00:23
Galerinha, eu não entendi a questão A...
Ela não se refere apenas a quantidade arrecada em função de x?

A formula não seria então Q= 10,00 . x?
-
valeriamsa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 26, 2011 23:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por demolot » Sex Mai 27, 2011 08:31
por demolot » Sex Mai 27, 2011 08:31
Nao visto que Q(x)= é quantidade de dinheiro arrecadado a funçao tem obrigatoriamente que ter o 12*6 +10x
-
demolot
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Dez 11, 2010 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Informatica
- Andamento: cursando
 por Claudin » Sex Mai 27, 2011 09:36
por Claudin » Sex Mai 27, 2011 09:36
a)

horamarcada --> R$12,00 . 6 clientes fixos/ R$10,00 . X (clientes variáveis por dia).
b) Sendo 6 clientes com hora marcada, e 10 com hora não marcada totalizando 16.
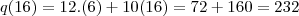
c)
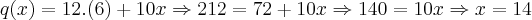
Seriam 14 clientes, quando o faturamento for de R$ 212,00.
d)
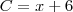
Seriam 6 clientes fixos por dia, mais o valor variável dos que não marcam hora.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por valeriamsa » Sex Mai 27, 2011 19:19
por valeriamsa » Sex Mai 27, 2011 19:19
Valeu pessoal!!! Muito obrigada!
-
valeriamsa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 26, 2011 23:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por valeriamsa » Dom Mai 29, 2011 23:11
por valeriamsa » Dom Mai 29, 2011 23:11
Não consigo postar uma duvida separada de uma questão ja existente...

Dada a função f :R-R defenida por f(x)= ax + b com a, b E R calcular a e b sabendo que f(2)=3 e f(3)=9. Determine a função.
Não tenho ideia de como fazer isso visto que a formula não me da o valor nem de a e nem de b...

-
valeriamsa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mai 26, 2011 23:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite ?, ?] Dúvida num pequeno passo
por Imscatman » Ter Set 27, 2011 22:56
- 2 Respostas
- 1283 Exibições
- Última mensagem por Imscatman

Qua Set 28, 2011 15:46
Cálculo: Limites, Derivadas e Integrais
-
- Problema com função
por Bia_Oliveira » Qui Set 20, 2012 10:41
- 3 Respostas
- 4654 Exibições
- Última mensagem por Cleyson007

Sex Set 21, 2012 11:05
Funções
-
- [Problema com Função] problema de função Help!
por [ddxprj] » Dom Mai 19, 2013 14:58
- 0 Respostas
- 1070 Exibições
- Última mensagem por [ddxprj]

Dom Mai 19, 2013 14:58
Funções
-
- problema de função
por rcpn » Qui Abr 10, 2014 11:15
- 3 Respostas
- 4906 Exibições
- Última mensagem por Russman

Sex Abr 11, 2014 17:30
Álgebra Elementar
-
- Problema de função
por zenildo » Qua Jul 15, 2015 00:11
- 2 Respostas
- 2318 Exibições
- Última mensagem por zenildo

Qua Jul 15, 2015 11:01
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 horamarcada --> R$12,00 . 6 clientes fixos/ R$10,00 . X (clientes variáveis por dia).
horamarcada --> R$12,00 . 6 clientes fixos/ R$10,00 . X (clientes variáveis por dia).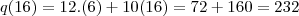
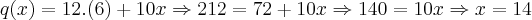 Seriam 14 clientes, quando o faturamento for de R$ 212,00.
Seriam 14 clientes, quando o faturamento for de R$ 212,00.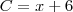 Seriam 6 clientes fixos por dia, mais o valor variável dos que não marcam hora.
Seriam 6 clientes fixos por dia, mais o valor variável dos que não marcam hora.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.