Um cabeleireiro cobra R$ 12,00 pelo corte para clientes com hora marcada e R$ 10,00 para clientes sem hora marcada. Ele atende por dia um número fixo de 6 clientes com hora marcada e um número variável x de clientes sem hora marcada .
a) escreva a fórmula matemática que fornece a quantia Q arrecadada por dia em função do numero x .
b) Qual foi a quantia arrecada num dia em que foram atendidos 16 clientes ?
c) Qual foi o numero de clientes atendidos num dia em que foram arrecadados R$ 212,00 ?
d) Qual é a expressão que indica o numero C de clientes atendidos por dia em função de x ?
horamarcada --> R$12,00 . 6 clientes fixos/ R$10,00 . X (clientes variáveis por dia).
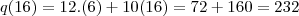
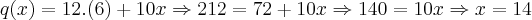Seriam 14 clientes, quando o faturamento for de R$ 212,00.
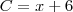Seriam 6 clientes fixos por dia, mais o valor variável dos que não marcam hora.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)