Olá
Gostaria de uma ajuda sobre inequação potência. Sei que existem inequação potência com expoente par e ímpar. A de expoente ímpar eu entendir. Pois a inequação potência de expoente ímpar tem sempre o sinal da base, de acordo com esses exemplos:
(x - 4)^7 <= 0 ==> x - 4 <= 0 ==> x <= 4
(3x - 1)^1001 >= 0 ==> 3x - 1>= 0 ==> x >= 1/3
Agora não entendi as inequação de expoente par, gostaria de uma ajuda de como resolvê-las, eis uns exemplos:
(7 - 3x)^4 < 0
(2x - 1)^100 >= 0
Gostaria de saber como resolver as inequações potência de expoente par.
Obrigado.



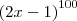
 0 ,No livro em que estudo traz a seguinte resposta: S = R , gostaria de saber porque essa resposta S = R. Se puder me responder, agradeço.
0 ,No livro em que estudo traz a seguinte resposta: S = R , gostaria de saber porque essa resposta S = R. Se puder me responder, agradeço.
 ou seja, impossível, como você já explicou acima.
ou seja, impossível, como você já explicou acima. 0 ------> 3x – 6
0 ------> 3x – 6 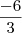 ----- > x = -2
----- > x = -2![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.