 por brumadense » Sex Jan 22, 2010 00:34
por brumadense » Sex Jan 22, 2010 00:34
Olá
Gostaria de uma ajuda sobre inequação potência. Sei que existem inequação potência com expoente par e ímpar. A de expoente ímpar eu entendir. Pois a inequação potência de expoente ímpar tem sempre o sinal da base, de acordo com esses exemplos:
(x - 4)^7 <= 0 ==> x - 4 <= 0 ==> x <= 4
(3x - 1)^1001 >= 0 ==> 3x - 1>= 0 ==> x >= 1/3
Agora não entendi as inequação de expoente par, gostaria de uma ajuda de como resolvê-las, eis uns exemplos:
(7 - 3x)^4 < 0
(2x - 1)^100 >= 0
Gostaria de saber como resolver as inequações potência de expoente par.
Obrigado.
-
brumadense
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jan 15, 2010 00:06
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Elcioschin » Sex Jan 22, 2010 09:11
por Elcioschin » Sex Jan 22, 2010 09:11
Um número real (positivo ou negativo) elevado a um expoente par será sempre POSITIVO.
Logo: (7 - 3x)^4 < 0 é IMPOSSÌVEL.
O outro dá para resolver:
(2x - 1)^100 >= 0 ----> (2x - 1)^100 = 0 -----> 2x - 1 = 0 ----> x = 1/2 ----> Solução geral -----> x >= 1/2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por brumadense » Qui Jan 28, 2010 02:58
por brumadense » Qui Jan 28, 2010 02:58
Elcioschin escreveu:Um número real (positivo ou negativo) elevado a um expoente par será sempre POSITIVO.
Logo: (7-3x)^4 < 0 é IMPOSSÌVEL.
O outro dá para resolver:
(2x-1)^100 >= 0 ----> (2x-1)^100 = 0 -----> 2x - 1 = 0 ----> x = 1/2 ----> Solução geral -----> x >= 1/2
Olá Elcioschin, obrigado pela resposta.
A primeira questão eu entendi, agora gostaria de saber se poderia me ajudar nessas outras questões:
A segunda questão:
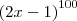

0 ,No livro em que estudo traz a seguinte resposta: S = R , gostaria de saber porque essa resposta S = R. Se puder me responder, agradeço.
Agora nessas questões:


0 ----> S = R , também não entendi do porque do S = R
Nessa outra questão:

> 0 ------> S = R – {2} , não entendi porque deu R – {2}
Essa questão:

< 0 ----- S =

ou seja, impossível, como você já explicou acima.
Agora essa outra questão:


0 ------> 3x – 6

0 ------> x =
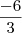
----- > x = -2
No livro traz S = {2}
Agora não entendi do por quê deu 2 e não menos -2 , será que tem a ver com o sinal de = (igualdade) que acompanha o sinal de < (maior).
Desde já agradeço.
-
brumadense
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jan 15, 2010 00:06
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Elcioschin » Qui Jan 28, 2010 09:16
por Elcioschin » Qui Jan 28, 2010 09:16
Lembre-se do que eu expliquei antes:
TODA expressão REAL na variável x elevada a expoente PAR nunca será negativa.
Assim ----> (2x - 1)^100 nunca será NEGATIVA.
Logo ----> (2x - 1)^100 = 0 ----> é POSSÍVEL para x = 1/2 ----> (2x - 1)^100 > 0 é POSSÍVEL para qualquer valor de x
Logo a solução para (2x - 1) >= 0 é sempre possível, para QUALQUER valor REAL de x ----> {R}
Vamos agora ver o outro:
(3x - 6)^6 =< 0 ----> temos DUAS opções:
1) (3x - 6)^6 < 0 -----> IMPOSSÍVEL
2) (3x - 6)^6 = 0 -----> 3x - 6 = 0 ----> 3x = 6 ----> x = 6/3 ----> x = 2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3770 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8610 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Potenciação - Potência de potência
por Ana Paula MMS » Sáb Jan 11, 2014 14:59
- 1 Respostas
- 2631 Exibições
- Última mensagem por Cleyson007

Sáb Jan 11, 2014 17:27
Aritmética
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2039 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



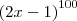
 0 ,No livro em que estudo traz a seguinte resposta: S = R , gostaria de saber porque essa resposta S = R. Se puder me responder, agradeço.
0 ,No livro em que estudo traz a seguinte resposta: S = R , gostaria de saber porque essa resposta S = R. Se puder me responder, agradeço.
 ou seja, impossível, como você já explicou acima.
ou seja, impossível, como você já explicou acima. 0 ------> 3x – 6
0 ------> 3x – 6 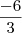 ----- > x = -2
----- > x = -2




