 por jeferson_justo135 » Seg Jan 12, 2015 22:48
por jeferson_justo135 » Seg Jan 12, 2015 22:48
Calcular a transformada de laplace das seguintes funções:
a)

=
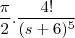
=
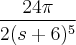
b)
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi t) \sqrt[]{5}.{e}^{-8t}.cos(3\pi t)](/latexrender/pictures/4d42b208c0a1ab0dde0f230257218d0c.png)
=
![\sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}} \sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}}](/latexrender/pictures/604ad6648ad43987a7b5d73fbe8b5fcf.png)
=

c)
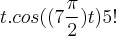
= eliminando os parênteses fica =

=
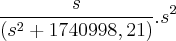
Pessoal por favor, estou com dúvidas, alguém pode me dizer se eu acertei os três exercícios? Obrigado.
-
jeferson_justo135
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 12, 2015 20:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por Russman » Ter Jan 13, 2015 02:22
por Russman » Ter Jan 13, 2015 02:22
A letra a) está correta.
Na letra b) você usou a Transformada da Função

.
De fato,
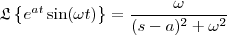
enquanto
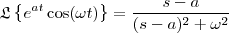
.
A letra c) está errada. Uma vez que você conhece a Transformada da função

, utilize do fato de que
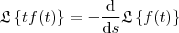
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jeferson_justo135 » Ter Jan 13, 2015 21:04
por jeferson_justo135 » Ter Jan 13, 2015 21:04
Muito obrigado pelo retorno! Refiz os itens b e c porém surgiram dúvidas:
b)
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi.t)=\frac{s+8}{({s+8}^{2})+3{\pi}^{2}}=\frac{s+8}{{s}^{2}+16s+152,83} \sqrt[]{5}.{e}^{-8t}.cos(3\pi.t)=\frac{s+8}{({s+8}^{2})+3{\pi}^{2}}=\frac{s+8}{{s}^{2}+16s+152,83}](/latexrender/pictures/2eba32dbae5bfce92ac0039622024e21.png)
= está correto?
c)

= não consegui entender o que você disse para aplicar, você pode me mostrar por favor? Estou aprendendo agora essa matéria.
Obrigado.
-
jeferson_justo135
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 12, 2015 20:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por Russman » Qua Jan 14, 2015 01:52
por Russman » Qua Jan 14, 2015 01:52
Agora a letra b) está correta. Você não precisa expandir os termos e muito menos substituir um valor aproximado de

. É perfeitamente correto que
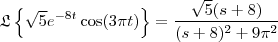
Para calcular a transformada da função da letra c) você pode usar a propriedade
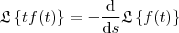
.
Esta diz que se você tem uma função

, sabe a sua Transformada e deseja calcular a transformada desta função multiplicada por

então basta derivar com respeito a

a Transfomada de

e trocar o sinal.
Por exemplo, gostaríamos de calcular a Transformada de
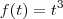
. De fato,
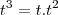
e

.
Assim, segundo a propriedade,
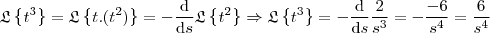
Entende?
Não é difícil de mostrar esse propriedade.
A Transformada
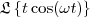
será
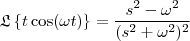
.
Tente resolver e concluir a afirma a cima.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por jeferson_justo135 » Qui Jan 15, 2015 09:22
por jeferson_justo135 » Qui Jan 15, 2015 09:22
Muito obrigado novamente! Eu vou refazer e ainda hoje posto o resultado para verificação!
-
jeferson_justo135
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 12, 2015 20:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por jeferson_justo135 » Seg Jan 19, 2015 16:55
por jeferson_justo135 » Seg Jan 19, 2015 16:55
Olá amigo muito obrigado!
Eu refiz os cálculos e consegui chegar nesse resultado, porém surgiu uma dúvida: a parte de cima da equação final
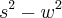
foi resultado de uma derivada assim como a parte de baixo? Pois na verdade o que aparenta é que foi derivado apenas a parte de baixo e a de cima foi alterado apenas o sinal.
Obrigado.
-
jeferson_justo135
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 12, 2015 20:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por jeferson_justo135 » Dom Fev 08, 2015 16:53
por jeferson_justo135 » Dom Fev 08, 2015 16:53
Olá amigo, refiz o item c com suas dicas, cheguei a esse resultado:
Transformada de
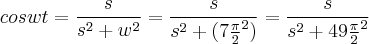
Transformada de

Logo a trasnformada de Laplace de

Por favor, agora está certo?
No item a, posso simplificar o resultado de
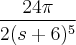
por

?
Obrigado.
-
jeferson_justo135
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 12, 2015 20:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [TRANSFORMADA DE LAPLACE]
 por liviabgomes » Qui Dez 01, 2011 15:19
por liviabgomes » Qui Dez 01, 2011 15:19
- 1 Respostas
- 1217 Exibições
- Última mensagem por LuizAquino

Seg Dez 05, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
-
- Transformada de Laplace
por Russman » Sex Mai 04, 2012 01:13
- 2 Respostas
- 1578 Exibições
- Última mensagem por pvgomes07

Sex Ago 10, 2012 13:11
Funções
-
- transformada de laplace
por theSinister » Seg Nov 05, 2012 16:01
- 2 Respostas
- 1244 Exibições
- Última mensagem por theSinister

Seg Nov 05, 2012 18:11
Cálculo: Limites, Derivadas e Integrais
-
- Transformada de Laplace - função de transferência
por pvgomes07 » Sex Ago 10, 2012 12:52
- 2 Respostas
- 1610 Exibições
- Última mensagem por pvgomes07

Qui Ago 16, 2012 15:40
Cálculo: Limites, Derivadas e Integrais
-
- coordenadas esfericas Laplace tridimensional
por rhuam » Sex Set 15, 2017 09:36
- 0 Respostas
- 1830 Exibições
- Última mensagem por rhuam

Sex Set 15, 2017 09:36
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 =
= 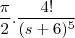 =
= 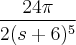
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi t) \sqrt[]{5}.{e}^{-8t}.cos(3\pi t)](/latexrender/pictures/4d42b208c0a1ab0dde0f230257218d0c.png) =
= ![\sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}} \sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}}](/latexrender/pictures/604ad6648ad43987a7b5d73fbe8b5fcf.png) =
= 
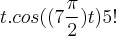 = eliminando os parênteses fica =
= eliminando os parênteses fica =  =
= 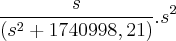

 =
= 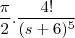 =
= 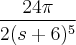
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi t) \sqrt[]{5}.{e}^{-8t}.cos(3\pi t)](/latexrender/pictures/4d42b208c0a1ab0dde0f230257218d0c.png) =
= ![\sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}} \sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}}](/latexrender/pictures/604ad6648ad43987a7b5d73fbe8b5fcf.png) =
= 
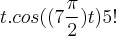 = eliminando os parênteses fica =
= eliminando os parênteses fica =  =
= 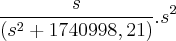

 .
. 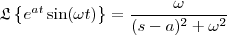
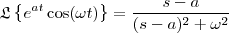 .
. , utilize do fato de que
, utilize do fato de que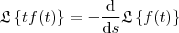 .
.
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi.t)=\frac{s+8}{({s+8}^{2})+3{\pi}^{2}}=\frac{s+8}{{s}^{2}+16s+152,83} \sqrt[]{5}.{e}^{-8t}.cos(3\pi.t)=\frac{s+8}{({s+8}^{2})+3{\pi}^{2}}=\frac{s+8}{{s}^{2}+16s+152,83}](/latexrender/pictures/2eba32dbae5bfce92ac0039622024e21.png) = está correto?
= está correto? = não consegui entender o que você disse para aplicar, você pode me mostrar por favor? Estou aprendendo agora essa matéria.
= não consegui entender o que você disse para aplicar, você pode me mostrar por favor? Estou aprendendo agora essa matéria.
 . É perfeitamente correto que
. É perfeitamente correto que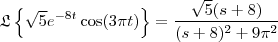
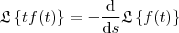 .
. , sabe a sua Transformada e deseja calcular a transformada desta função multiplicada por
, sabe a sua Transformada e deseja calcular a transformada desta função multiplicada por  então basta derivar com respeito a
então basta derivar com respeito a  a Transfomada de
a Transfomada de  e trocar o sinal.
e trocar o sinal.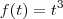 . De fato,
. De fato, 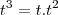 e
e  .
.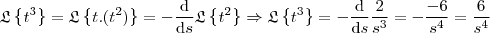
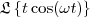 será
será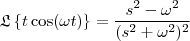 .
.

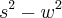 foi resultado de uma derivada assim como a parte de baixo? Pois na verdade o que aparenta é que foi derivado apenas a parte de baixo e a de cima foi alterado apenas o sinal.
foi resultado de uma derivada assim como a parte de baixo? Pois na verdade o que aparenta é que foi derivado apenas a parte de baixo e a de cima foi alterado apenas o sinal.

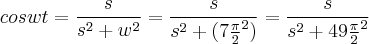


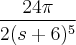 por
por  ?
?