a)
 =
= 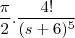 =
= 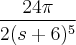
b)
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi t) \sqrt[]{5}.{e}^{-8t}.cos(3\pi t)](/latexrender/pictures/4d42b208c0a1ab0dde0f230257218d0c.png) =
= ![\sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}} \sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}}](/latexrender/pictures/604ad6648ad43987a7b5d73fbe8b5fcf.png) =
= 
c)
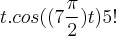 = eliminando os parênteses fica =
= eliminando os parênteses fica =  =
= 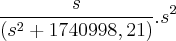
Pessoal por favor, estou com dúvidas, alguém pode me dizer se eu acertei os três exercícios? Obrigado.

 =
= 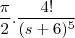 =
= 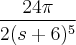
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi t) \sqrt[]{5}.{e}^{-8t}.cos(3\pi t)](/latexrender/pictures/4d42b208c0a1ab0dde0f230257218d0c.png) =
= ![\sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}} \sqrt[]{5}.\frac{3\pi}{{(s+8)}^{2}+{3\pi}^{2}}](/latexrender/pictures/604ad6648ad43987a7b5d73fbe8b5fcf.png) =
= 
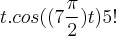 = eliminando os parênteses fica =
= eliminando os parênteses fica =  =
= 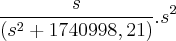

 .
. 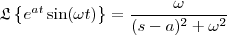
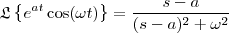 .
. , utilize do fato de que
, utilize do fato de que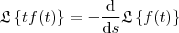 .
.
![\sqrt[]{5}.{e}^{-8t}.cos(3\pi.t)=\frac{s+8}{({s+8}^{2})+3{\pi}^{2}}=\frac{s+8}{{s}^{2}+16s+152,83} \sqrt[]{5}.{e}^{-8t}.cos(3\pi.t)=\frac{s+8}{({s+8}^{2})+3{\pi}^{2}}=\frac{s+8}{{s}^{2}+16s+152,83}](/latexrender/pictures/2eba32dbae5bfce92ac0039622024e21.png) = está correto?
= está correto? = não consegui entender o que você disse para aplicar, você pode me mostrar por favor? Estou aprendendo agora essa matéria.
= não consegui entender o que você disse para aplicar, você pode me mostrar por favor? Estou aprendendo agora essa matéria.
 . É perfeitamente correto que
. É perfeitamente correto que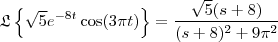
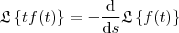 .
. , sabe a sua Transformada e deseja calcular a transformada desta função multiplicada por
, sabe a sua Transformada e deseja calcular a transformada desta função multiplicada por  então basta derivar com respeito a
então basta derivar com respeito a  a Transfomada de
a Transfomada de  e trocar o sinal.
e trocar o sinal.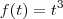 . De fato,
. De fato, 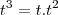 e
e  .
.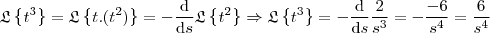
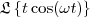 será
será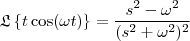 .
.

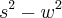 foi resultado de uma derivada assim como a parte de baixo? Pois na verdade o que aparenta é que foi derivado apenas a parte de baixo e a de cima foi alterado apenas o sinal.
foi resultado de uma derivada assim como a parte de baixo? Pois na verdade o que aparenta é que foi derivado apenas a parte de baixo e a de cima foi alterado apenas o sinal.

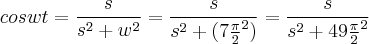


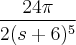 por
por  ?
?
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
