Nossa! Me desculpe, quando estava digitando nem havia percebido...houve um pequeno erro de digitação na função a ser integrada ao escrevê-la em LATEX.
a função f quando sobre um 3 sei que pode ser simplificada com meios bem básicos de integração.
Mas quando se tem um (...)/x tem a necessidade de uma substituição correto?
Obs: Já arrumei a função. da minha dúvida.
E estive usando como referência o Geogebra para tentar chegar a solução, mas algo ainda devo estar fazendo errado, pois: a solução dada por ele é
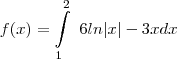
Sendo que no máximo pelo que tentei até 3horas atrás fora:
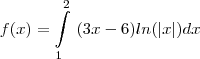
Sei que meu cálculo está errado e pensei que talvez seja por conta do valor da substituição não ter sido a melhor escolha, mas se fosse 1/x sei que teria sido pior.
portanto usei a partir de
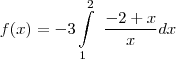
u = x - 2

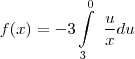
![f(x)=-3[uln(|x|)]\int\limits_{1}^2 f(x)=-3[uln(|x|)]\int\limits_{1}^2](/latexrender/pictures/c4f38fb87d6d8071e42e0f6a46fb7ad3.png)
![f(x)=-3(x - 2)ln(|x|)]\int\limits_{1}^2 f(x)=-3(x - 2)ln(|x|)]\int\limits_{1}^2](/latexrender/pictures/6f92babf4a802b3ae51f036aa583e04a.png)
mas, -3ln|x|u = -3(x - 2)ln|x| =-3x + 6ln|x|
Assim:
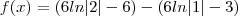



Está tudo ok?
Acho que saquei o que eu estava errando. A volta da substituição de u para x, estava a fazer toda vez a volta para x com as parênteses e acaba por pensar que tinha distributiva aonde nada havia.
![f(x)=\int\limits_{1}^2~[(6-3x)/x] dx f(x)=\int\limits_{1}^2~[(6-3x)/x] dx](/latexrender/pictures/e7be5d9ba5fca038aac3a38e5ba3eb0b.png)


![\\ f(x) = \int_{1}^{2} \left [ \frac{(6 - 3x)}{3} \right ] dx = \\\\\\ f(x) = \int_{1}^{2} \frac{3(2 - x)}{3} dx = \\\\\\ f(x) = \int_{1}^{2} (2 - x) dx = \\ f(x) = \int_{1}^{2} \left [ \frac{(6 - 3x)}{3} \right ] dx = \\\\\\ f(x) = \int_{1}^{2} \frac{3(2 - x)}{3} dx = \\\\\\ f(x) = \int_{1}^{2} (2 - x) dx =](/latexrender/pictures/93a996dcb59d7eb38e132534bd08d81b.png)

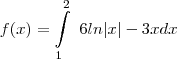
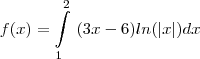
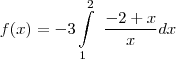

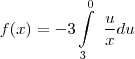
![f(x)=-3[uln(|x|)]\int\limits_{1}^2 f(x)=-3[uln(|x|)]\int\limits_{1}^2](/latexrender/pictures/c4f38fb87d6d8071e42e0f6a46fb7ad3.png)
![f(x)=-3(x - 2)ln(|x|)]\int\limits_{1}^2 f(x)=-3(x - 2)ln(|x|)]\int\limits_{1}^2](/latexrender/pictures/6f92babf4a802b3ae51f036aa583e04a.png) mas, -3ln|x|u = -3(x - 2)ln|x| =-3x + 6ln|x|
mas, -3ln|x|u = -3(x - 2)ln|x| =-3x + 6ln|x|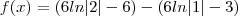



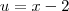 . Deverias ter substituído
. Deverias ter substituído  por
por  , pois
, pois  .
.![\\ f(x) = \int_{1}^{2} \frac{6 - 3x}{x} dx \\\\\\ f(x) = \int_{1}^{2} \frac{6}{x} - \frac{3x}{x} dx \\\\\\ f(x) = \int_{1}^{2} \frac{6}{x} dx - \int_{1}^{2} \frac{3\cancel{x}}{\cancel{x}} dx \\\\\\ f(x) = 6 \cdot \int_{1}^{2} \frac{1}{x} dx - 3 \cdot \int_{1}^{2} dx \\\\\\ f(x) = 6 \cdot \left[ \ln x \right]_{1}^{2} - 3 \cdot \left[ x \right]_{1}^{2} \\\\ (...) \\ f(x) = \int_{1}^{2} \frac{6 - 3x}{x} dx \\\\\\ f(x) = \int_{1}^{2} \frac{6}{x} - \frac{3x}{x} dx \\\\\\ f(x) = \int_{1}^{2} \frac{6}{x} dx - \int_{1}^{2} \frac{3\cancel{x}}{\cancel{x}} dx \\\\\\ f(x) = 6 \cdot \int_{1}^{2} \frac{1}{x} dx - 3 \cdot \int_{1}^{2} dx \\\\\\ f(x) = 6 \cdot \left[ \ln x \right]_{1}^{2} - 3 \cdot \left[ x \right]_{1}^{2} \\\\ (...)](/latexrender/pictures/1fe860bee519d8a675d1f53c3a7c6212.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.