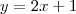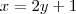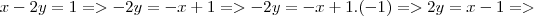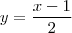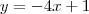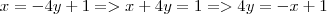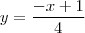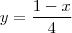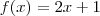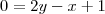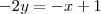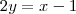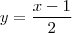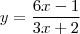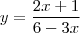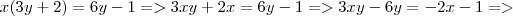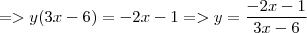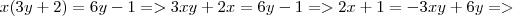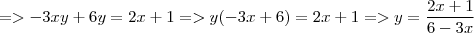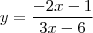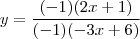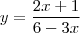por Reavourz » Qui Jul 10, 2014 17:21
por Reavourz » Qui Jul 10, 2014 17:21
Olá pessoal estou com uma dúvida na parte da equação, bom vamos lá.
Exemplo:
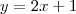
Eu substituí o y por x e o x por y ficando assim:
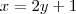
Resolução:
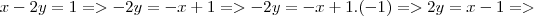
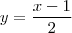
Ai estava eu pesquisando algumas coisas vi isso em um site.
Para determinar a função inversa de f(x)=2x+1 basta:
y=2x+1 (trocar x por y)
x=2y+1 (isolar o y)
-2y= – x+1
(O +1 não deveria virar -1)? 2y= x+1
( COMO PODE ISSO?) y=(x+1)/2
f-¹(x)=(x+1)/2
Em meu livro também tem um parecido:
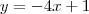
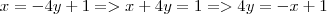
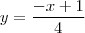
no livro o resultado é
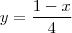
Desde já agradeço.
-
Reavourz
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jun 13, 2014 22:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qui Jul 10, 2014 21:17
por young_jedi » Qui Jul 10, 2014 21:17
a primeira função que voce posto
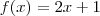
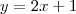
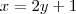
agora passando o x para o lado esquerdo da equação
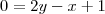
e passando o y para o lado direito
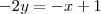
multiplicando a equação por -1
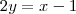
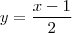
realmente a resposta apontada esta errada
agora o segundo caso
o resultado encontrado foi
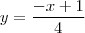
que é a mesma coisa que
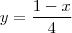
esta correto não tem nenhuma incoerencia
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Reavourz » Qui Jul 10, 2014 23:37
por Reavourz » Qui Jul 10, 2014 23:37
vlw cara pensei que estava errado minha resolução, pois essa Y=(x+1)/2 eu vi em um site que estava tratando de funções inversas, tenso quem aprendeu por lá aprendeu errado. Obrigado pela ajuda.
Pode me ajudar nesta aqui?
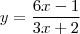
Bom o gabarito do livro está:
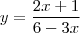
Eu fiz a primeira resolução:
Não consigo enxergar o que tem de errado aqui.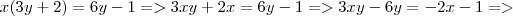
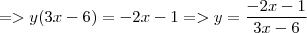
Fiz depois a segunda:
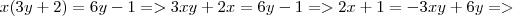
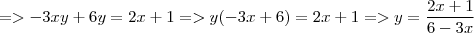
Não sei o que estou fazendo de errado pois na
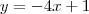
deu das duas formas, tanto passando 4x positivo, como deixando negativo.
-
Reavourz
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jun 13, 2014 22:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Reavourz » Sáb Jul 12, 2014 00:11
por Reavourz » Sáb Jul 12, 2014 00:11
vlw cara me ajudou muito, não tinha me ligado de aplicar o (-1) na fração vlw, muito obrigado.
-
Reavourz
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jun 13, 2014 22:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3401 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- O que é função inversa
por irineu junior » Sex Mar 12, 2010 20:57
- 2 Respostas
- 2644 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 16:28
Funções
-
- Função Inversa
por OtavioBonassi » Qui Jul 14, 2011 23:04
- 6 Respostas
- 7731 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:14
Funções
-
- Função Inversa.
por jcvalim » Qua Ago 24, 2011 15:57
- 0 Respostas
- 1186 Exibições
- Última mensagem por jcvalim

Qua Ago 24, 2011 15:57
Funções
-
- função inversa
por tigre matematico » Qui Out 13, 2011 12:45
- 1 Respostas
- 2214 Exibições
- Última mensagem por Guill

Sáb Abr 21, 2012 18:07
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.