Vou começar postando aqui a primeira prova do trimestre, que acertei 4 de 10 questões, é sobre números complexos:
E claro, aproveitei para revisar algumas das contas, espero ter acertado agora.
Peço a ajuda de todos vocês para me ajudar a entender de uma vez por todas essa matéria. Preciso muito passar de ano, já estou desesperado. Leiam novamente a primeira linha desse post para entenderem o drama.
1) Dê as condições sobre os reais
 e
e  para que o número complexo
para que o número complexo  seja:
seja:a) Imaginário Puro
RESPOSTA:



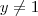
b) Real
RESPOSTA:

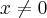


----
2) Dados
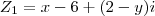 e
e 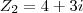 , encontre
, encontre  e
e  para que
para que 
RESPOSTA:

Apliquei a igualdade de números complexos, e o resultado foi:


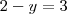
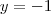
----
3) Determine o número complexo
 tal que
tal que 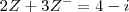
RESPOSTA:
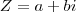


(o n° 1 abaixo não aparece na conta, mas está multiplicando o
 )
)
(somando os termos semelhantes)
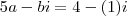
(e agora aplicando a igualdade de números complexos)

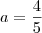


----
4) Qual o conjugado do n° complexo
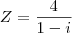 ?
?RESPOSTA:
(Aqui eu só multipliquei a fração pelo conjugado do denominador, não sei se fiz certo.)
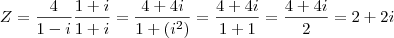
----
5) Dados os números complexos
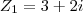 e
e  , qual é o valor de
, qual é o valor de  ?
?(essa eu não respondi na prova, infelizmente. Mas vou tentar aqui.)
RESPOSTA:
Primeiro, multiplico
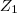 por
por 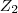 , certo?
, certo?Ficaria
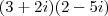
que teria como resposta

Juntando os termos...

E na conta, agora temos:

Então eu aplico aquela fórmula:
![|Z|=\sqrt[]{6^2-21^2} |Z|=\sqrt[]{6^2-21^2}](/latexrender/pictures/d9022554abaf630d0b91232881237e37.png)
![\sqrt[]{36-441} \sqrt[]{36-441}](/latexrender/pictures/3e8e4272075fe9fd081832e4c0a893f1.png)
![\sqrt[]{405} \sqrt[]{405}](/latexrender/pictures/b144be029ef40b3bd692daf7c4b0ce6e.png)
E agora,
![| \sqrt[]{405} |^2=405 | \sqrt[]{405} |^2=405](/latexrender/pictures/6927d3e004675bd6aa0d847fa15da8d1.png)
Acertei?

----
6) Um número complexo
 e seu conjugado são tais que
e seu conjugado são tais que  e
e  . Qual a forma trigonométrica de
. Qual a forma trigonométrica de  ?
?(essa eu também não fiz na prova D:)
RESPOSTA:
Bom, observando bem a conta, me parece mais lógico resolvê-la assim:
{

{
 < deu zero o__o (empaquei aqui)
< deu zero o__o (empaquei aqui)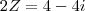
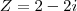 < usei isso para continuar a conta acima citada ^
< usei isso para continuar a conta acima citada ^----
7) Coloque na forma algébrica o complexo:
![2\sqrt[]{2}( 2\sqrt[]{2}(](/latexrender/pictures/c4366d6138dd7cc1bf684fcd91a680c9.png) cos
cos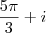 sen
sen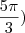
(um
 no meio da conta?!
no meio da conta?!Nunca vi isso.)
Alguém poderia resolver essa?

----
8) Determine
 e
e  de modo que
de modo que 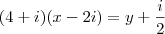
RESPOSTA:

(Passei aquele denominador da fração pra o outro lado, para multiplicar)

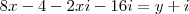
(Agora, tenho que encontrar o X)

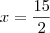
(Ainda me falta o Y)
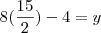

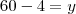

Logo,
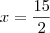

----
... Ainda tenho mais duas provas para postar aqui, e tenho pouco tempo D:
Muito obrigado pela atenção.



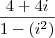 . Se fosse
. Se fosse  , resultaria em
, resultaria em 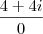 , um verdadeiro crime.
, um verdadeiro crime. , que é a forma trigonométrica (lembrando que
, que é a forma trigonométrica (lembrando que 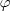 é o módulo de
é o módulo de 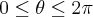 .
.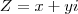 .
. 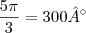 .
.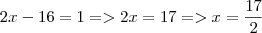 . Substituindo na equação (2) que é
. Substituindo na equação (2) que é  .
.



 seja o conjugado de Z, é isso mesmo, não é?
seja o conjugado de Z, é isso mesmo, não é?


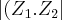
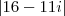


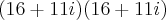







![\left|Z \right|=\sqrt[2]{{a}^{2}+{b}^{2}} \left|Z \right|=\sqrt[2]{{a}^{2}+{b}^{2}}](/latexrender/pictures/9c7ec8b0945dc08ed4ec1492f1f9378b.png)
![\left|Z \right|=2\sqrt[2]{3} \left|Z \right|=2\sqrt[2]{3}](/latexrender/pictures/0e455e46b12a64b0fca427dc05b62730.png)

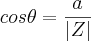

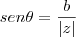
![cos\theta=\frac{\sqrt[2]{3}}{3} cos\theta=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/32234c19201b709bbc73ba1986920f64.png)
![sen\theta=\frac{-\sqrt[2]{3}}{3} sen\theta=\frac{-\sqrt[2]{3}}{3}](/latexrender/pictures/365488d905606b85b5ea1e85c3ad26cb.png)
![Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i) Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i)](/latexrender/pictures/a58fcb10900ecfce160a756589eba7a8.png)




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.