 por SamKoen » Qua Dez 16, 2009 15:14
por SamKoen » Qua Dez 16, 2009 15:14
Preciso tirar a nota máxima (40,0) na prova de recuperação que minha querida professora marcou para amanhã de manhã, e só agora encontrei esse verdadeiro oasis de matemáticos que adoram resolver problemas.
Vou começar postando aqui a primeira prova do trimestre, que acertei 4 de 10 questões, é sobre números complexos:
E claro, aproveitei para revisar algumas das contas, espero ter acertado agora.
Peço a ajuda de todos vocês para me ajudar a entender de uma vez por todas essa matéria. Preciso muito passar de ano, já estou desesperado. Leiam novamente a primeira linha desse post para entenderem o drama.
1) Dê as condições sobre os reais

e

para que o número complexo

seja:
a) Imaginário Puro
RESPOSTA:


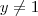
b) Real
RESPOSTA:
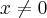


----
2) Dados
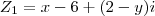
e
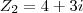
, encontre

e

para que
 RESPOSTA:
RESPOSTA:
Apliquei a igualdade de números complexos, e o resultado foi:


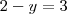
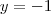
----
3) Determine o número complexo

tal que
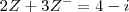 RESPOSTA:
RESPOSTA: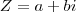


(o n° 1 abaixo não aparece na conta, mas está multiplicando o

)

(somando os termos semelhantes)
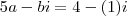
(e agora aplicando a igualdade de números complexos)

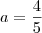


----
4) Qual o conjugado do n° complexo
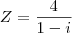
?
RESPOSTA:(Aqui eu só multipliquei a fração pelo conjugado do denominador, não sei se fiz certo.)
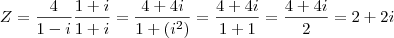
----
5) Dados os números complexos
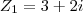
e

, qual é o valor de

?
(essa eu não respondi na prova, infelizmente. Mas vou tentar aqui.)
RESPOSTA:Primeiro, multiplico
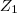
por
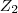
, certo?
Ficaria
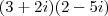
que teria como resposta

Juntando os termos...

E na conta, agora temos:

Então eu aplico aquela fórmula:
![|Z|=\sqrt[]{6^2-21^2} |Z|=\sqrt[]{6^2-21^2}](/latexrender/pictures/d9022554abaf630d0b91232881237e37.png)
![\sqrt[]{36-441} \sqrt[]{36-441}](/latexrender/pictures/3e8e4272075fe9fd081832e4c0a893f1.png)
![\sqrt[]{405} \sqrt[]{405}](/latexrender/pictures/b144be029ef40b3bd692daf7c4b0ce6e.png)
E agora,
![| \sqrt[]{405} |^2=405 | \sqrt[]{405} |^2=405](/latexrender/pictures/6927d3e004675bd6aa0d847fa15da8d1.png)
Acertei?

----
6) Um número complexo

e seu conjugado são tais que

e

. Qual a forma trigonométrica de

?
(essa eu também não fiz na prova D:)
RESPOSTA:Bom, observando bem a conta, me parece mais lógico resolvê-la assim:
{

{

< deu zero o__o (empaquei aqui)
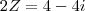
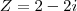
< usei isso para continuar a conta acima citada ^
----
7) Coloque na forma algébrica o complexo:
![2\sqrt[]{2}( 2\sqrt[]{2}(](/latexrender/pictures/c4366d6138dd7cc1bf684fcd91a680c9.png)
cos
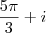
sen
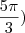
(um

no meio da conta?!
Nunca vi isso.)
Alguém poderia resolver essa?

----
8) Determine

e

de modo que
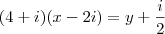 RESPOSTA:
RESPOSTA:
(Passei aquele denominador da fração pra o outro lado, para multiplicar)

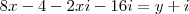
(Agora, tenho que encontrar o X)

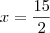
(Ainda me falta o Y)
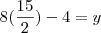

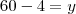

Logo,
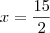

----
... Ainda tenho mais duas provas para postar aqui, e tenho pouco tempo D:
Muito obrigado pela atenção.
-
SamKoen
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Dez 16, 2009 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Dez 16, 2009 18:59
por MarceloFantini » Qua Dez 16, 2009 18:59
Questão 1, você acertou inteira.
Questão 2, você errou no seguinte:

Questão 3, você acertou inteira.
Questão 4, embora você tenha acertado o resultado, você errou ali na fatoração:
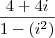
. Se fosse

, resultaria em
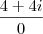
, um verdadeiro crime.
Questão 5, você acertou, se não me engano.
Questão 6, uma vez que você encontrou o complexo

, bastava você montar um pequeno gráfico com o ponto, encontrar o argumento e escrever

, que é a forma trigonométrica (lembrando que
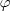
é o módulo de

, que é a distância do afixo até a origem, e que o argumento é o ângulo formado pelo módulo com a horizontal, onde
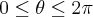
.
Questão 7 é basicamente fazer a volta. Ele te dá a forma trigonométrica e quer a equação na forma
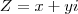
.
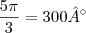
.
Questão 8, você fez uma bobeirinha na hora da conta:
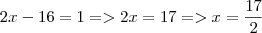
. Substituindo na equação (2) que é

.
Espero ter ajudado!
Um abraço, boa noite (e sucesso nas provas).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qua Dez 16, 2009 19:31
por Cleyson007 » Qua Dez 16, 2009 19:31
Boa tarde Sam Koen!
Quanto a primeira questão:a) Está resolvida corretamente. -->
Parece que você não apresenta dúvidas quanto a esse exercício.b) Está resolvida corretamente.
Quanto a segunda questão:Sam Koen, o princípio utilizado para resolução está correto. (observe o valor que você encontrou para x)

 (quando o sinal para o outro lado da igualdade ocorre a inversão do mesmo)
(quando o sinal para o outro lado da igualdade ocorre a inversão do mesmo)
O valor de y está correto.
Quanto a terceira questão:Sam Koen, estou considerando que

seja o conjugado de Z, é isso mesmo, não é?
Se for, sua resolução está correta!
Quanto a quarta questão:Sam Koen, o processo de resolução está correto!O conjugado de um número complexo fracionário é obtido multiplicando ambas as partes (numerador e denominador) pelo conjugado do denominador (sinal invertido da parte imaginária do denominador).
Quanto a quinta questão:Essa foi resolvida
ERRADA, veja:

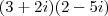



Como o enunciado pede
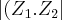
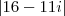


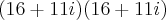
Resolvendo,

Vou te adiantar a resolução das cinco (05) primeiras questões que você postou. Daqui a pouco posto a resolução das outras.
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qua Dez 16, 2009 19:34
por MarceloFantini » Qua Dez 16, 2009 19:34
Perdão, eu estava errado sobre a questão 5. Siga o que o Cleyson falou!
Abraço, sucesso nas provas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qua Dez 16, 2009 19:57
por Cleyson007 » Qua Dez 16, 2009 19:57
Boa tarde Sam Koen e Fantini!
Fantini, que bom tê-la no Ajuda Matemática

Agradeço sua interação com o fórum!
Vai a resolução da questão 6:
Quanto a questão 6:Você encontrou o número complexo Z corretamente -->
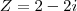
Vamos trabalhar com a Forma Trigonométrica de Z:

Para achar o valor de

![\left|Z \right|=\sqrt[2]{{a}^{2}+{b}^{2}} \left|Z \right|=\sqrt[2]{{a}^{2}+{b}^{2}}](/latexrender/pictures/9c7ec8b0945dc08ed4ec1492f1f9378b.png)
Resolvendo, encontra-se:
![\left|Z \right|=2\sqrt[2]{3} \left|Z \right|=2\sqrt[2]{3}](/latexrender/pictures/0e455e46b12a64b0fca427dc05b62730.png)
Para achar o

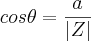
Para achar o

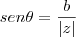
Com esses dados, você encontrará o valor do

![cos\theta=\frac{\sqrt[2]{3}}{3} cos\theta=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/32234c19201b709bbc73ba1986920f64.png)
E o

, será:
![sen\theta=\frac{-\sqrt[2]{3}}{3} sen\theta=\frac{-\sqrt[2]{3}}{3}](/latexrender/pictures/365488d905606b85b5ea1e85c3ad26cb.png)
Logo, na Forma Trigonométrica, tem-se:
![Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i) Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i)](/latexrender/pictures/a58fcb10900ecfce160a756589eba7a8.png)
![Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i) Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i)](/latexrender/pictures/a58fcb10900ecfce160a756589eba7a8.png)
Comente qualquer dúvida

Até mais.
Editado pela última vez por
Cleyson007 em Qua Dez 16, 2009 20:00, em um total de 1 vez.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qua Dez 16, 2009 20:00
por MarceloFantini » Qua Dez 16, 2009 20:00
Obrigado Cleyson, apenas um pequeno detalhe: tê-l
o.

Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qua Dez 16, 2009 20:02
por Cleyson007 » Qua Dez 16, 2009 20:02
Fantini escreveu:Obrigado Cleyson, apenas um pequeno detalhe: tê-l
o.

Um abraço.
Desculpe Fantini

Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por SamKoen » Sáb Dez 19, 2009 12:01
por SamKoen » Sáb Dez 19, 2009 12:01
Desculpem não ter postado antes, voltei ao fórum quando recebi as respostas, mas não postei nada. Reparei meus erros e voltei a estudar.
Passei de ano graças a vocês, Fantini e Cleyson. Vocês simplesmente me fizeram gabaritar aquela prova de matemática!
Fica aqui meu MUITO OBRIGADO e votos de SUCESSO a vocês e a todos do fórum

-
SamKoen
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Dez 16, 2009 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Seg Dez 21, 2009 18:47
por Cleyson007 » Seg Dez 21, 2009 18:47
Boa tarde Sam Koen!
Fico feliz em saber que conseguiu passar de ano, e mais ainda, que pude dar minha parcela de contribuição

Foi um prazer ajudar! (sempre que for do nosso alcance, pode ter certeza que o faremos)
Até mais.
Sucessos a você também!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- conjuntos (valendo uma caixa de bis!!)me oriente por favor!
por Fabricio dalla » Sáb Abr 09, 2011 20:12
- 1 Respostas
- 2365 Exibições
- Última mensagem por Pedro123

Dom Abr 10, 2011 00:31
Álgebra Elementar
-
- Problemas com equações do 2° Questão valendo 1 ponto
por jvpetrucci » Qui Mai 03, 2012 19:14
- 12 Respostas
- 6164 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 22:35
Sistemas de Equações
-
- Ajuda com Prova Recuperação
por cortelettirlz » Qui Set 01, 2011 17:48
- 6 Respostas
- 3366 Exibições
- Última mensagem por phvicari

Dom Set 04, 2011 03:48
Trigonometria
-
- Atividade de Recuperação - PRA AMANHÃ!!
por TuttyFrutty » Dom Set 13, 2015 13:40
- 4 Respostas
- 2748 Exibições
- Última mensagem por Cleyson007

Dom Set 13, 2015 19:02
Funções
-
- Prova de recuperação - Geometria III - MAT310 - 2006
 por admin » Qui Mai 01, 2008 15:53
por admin » Qui Mai 01, 2008 15:53
- 0 Respostas
- 2669 Exibições
- Última mensagem por admin

Qui Mai 01, 2008 15:53
Geometria III
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  para que o número complexo
para que o número complexo  seja:
seja:


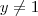

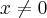


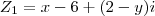 e
e 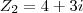 , encontre
, encontre  e
e  para que
para que 



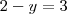
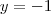
 tal que
tal que 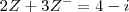
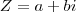


 )
)
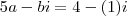

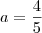


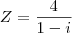 ?
?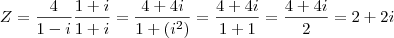
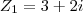 e
e  , qual é o valor de
, qual é o valor de  ?
?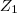 por
por 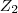 , certo?
, certo?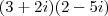



![|Z|=\sqrt[]{6^2-21^2} |Z|=\sqrt[]{6^2-21^2}](/latexrender/pictures/d9022554abaf630d0b91232881237e37.png)
![\sqrt[]{36-441} \sqrt[]{36-441}](/latexrender/pictures/3e8e4272075fe9fd081832e4c0a893f1.png)
![\sqrt[]{405} \sqrt[]{405}](/latexrender/pictures/b144be029ef40b3bd692daf7c4b0ce6e.png)
![| \sqrt[]{405} |^2=405 | \sqrt[]{405} |^2=405](/latexrender/pictures/6927d3e004675bd6aa0d847fa15da8d1.png)

 e seu conjugado são tais que
e seu conjugado são tais que  e
e  . Qual a forma trigonométrica de
. Qual a forma trigonométrica de  ?
?
 < deu zero o__o (empaquei aqui)
< deu zero o__o (empaquei aqui)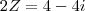
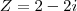 < usei isso para continuar a conta acima citada ^
< usei isso para continuar a conta acima citada ^![2\sqrt[]{2}( 2\sqrt[]{2}(](/latexrender/pictures/c4366d6138dd7cc1bf684fcd91a680c9.png) cos
cos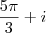 sen
sen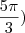
 no meio da conta?!
no meio da conta?!
 e
e  de modo que
de modo que 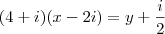


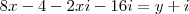

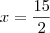
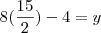

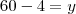

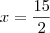




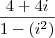 . Se fosse
. Se fosse  , resultaria em
, resultaria em 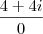 , um verdadeiro crime.
, um verdadeiro crime. , que é a forma trigonométrica (lembrando que
, que é a forma trigonométrica (lembrando que 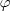 é o módulo de
é o módulo de 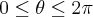 .
.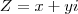 .
. 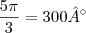 .
.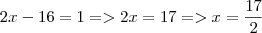 . Substituindo na equação (2) que é
. Substituindo na equação (2) que é  .
.



 seja o conjugado de Z, é isso mesmo, não é?
seja o conjugado de Z, é isso mesmo, não é?


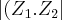
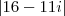


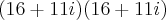







![\left|Z \right|=\sqrt[2]{{a}^{2}+{b}^{2}} \left|Z \right|=\sqrt[2]{{a}^{2}+{b}^{2}}](/latexrender/pictures/9c7ec8b0945dc08ed4ec1492f1f9378b.png)
![\left|Z \right|=2\sqrt[2]{3} \left|Z \right|=2\sqrt[2]{3}](/latexrender/pictures/0e455e46b12a64b0fca427dc05b62730.png)

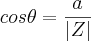

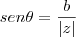
![cos\theta=\frac{\sqrt[2]{3}}{3} cos\theta=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/32234c19201b709bbc73ba1986920f64.png)
![sen\theta=\frac{-\sqrt[2]{3}}{3} sen\theta=\frac{-\sqrt[2]{3}}{3}](/latexrender/pictures/365488d905606b85b5ea1e85c3ad26cb.png)
![Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i) Z=2\sqrt[2]{3}(\frac{\sqrt[2]{3}}{3}-\frac{\sqrt[2]{3}}{3}i)](/latexrender/pictures/a58fcb10900ecfce160a756589eba7a8.png)


 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: