 por Ovelha » Ter Abr 15, 2014 16:09
por Ovelha » Ter Abr 15, 2014 16:09
Qual o coeficiente de

no desenvolvimento de
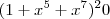
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Ter Abr 15, 2014 23:35
por e8group » Ter Abr 15, 2014 23:35
Deixe

em evidencia , teremos
![(1 + x^5 +x^7)^{20} = (1 +[x^5(1 +x^2)])^20 (1 + x^5 +x^7)^{20} = (1 +[x^5(1 +x^2)])^20](/latexrender/pictures/0ad7338f8254c716abb315c1a063622d.png)
.Pelo teorema binomial ,
![1 +[x^5(1 +x^2)])^20= \sum_{k=0}^{20} \binom{20}{k} [x^5(1+x^2)]^k = \sum_{k=0}^{20} \binom{20}{k} x^{5k}(1+x^2)^k = 1 + \binom{20}{1}x^5(1+x^2 ) + \binom{20}{2}x^{10}(1+x^2)^2 + \binom{20}{3}x^{15}(1 +x^2)^3 + \sum_{k=4}^{20} \binom{20}{k} [x^5(1+x^2)]^k 1 +[x^5(1 +x^2)])^20= \sum_{k=0}^{20} \binom{20}{k} [x^5(1+x^2)]^k = \sum_{k=0}^{20} \binom{20}{k} x^{5k}(1+x^2)^k = 1 + \binom{20}{1}x^5(1+x^2 ) + \binom{20}{2}x^{10}(1+x^2)^2 + \binom{20}{3}x^{15}(1 +x^2)^3 + \sum_{k=4}^{20} \binom{20}{k} [x^5(1+x^2)]^k](/latexrender/pictures/6b190677aa82f28ec474211533c54f62.png)
.
O termo
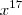
é oriundo da 4 parcela

. Basta desenvolver para encontrar o coefc.
Observe que nas parcelas ,

, o grau de x será sempre menor que

quando

(afinal de contas
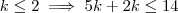
) e maior que

quando
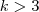
(afinal de contas
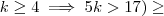
) .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Qua Abr 16, 2014 08:24
por Ovelha » Qua Abr 16, 2014 08:24
valeu pela ajuda, tô novo no assunto vou tentar desenvolver e se tiver problemas vou pedir sua ajuda, tudo bem?
Deus abençoe
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Qua Abr 16, 2014 10:19
por e8group » Qua Abr 16, 2014 10:19
Tranquilo , qualquer dúvida só dizer .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Qua Abr 16, 2014 13:16
por Ovelha » Qua Abr 16, 2014 13:16
Olá, tudo bem. Comecei a fazer agora não estou conseguindo passar da combinação, estou tendo problemas no desenvolvimento,não consigo visualizar como desenvolver.
Desculpe pelo aluguel
Deus abençoe
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Qua Abr 16, 2014 15:23
por e8group » Qua Abr 16, 2014 15:23
OK . :
Temos

e

. O único termo que nos interessa é

, pois
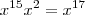
. Então o coefc. é
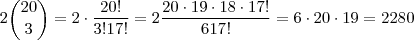
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Qui Abr 17, 2014 15:05
por Ovelha » Qui Abr 17, 2014 15:05
Valeu Santhiago, contudo eu estava olhando e descobri que as possiveis respostas da questão colocads como opção foram:
a) 0
b)3000
c)1210
d)3420
e)4000
Continuo contando com sua ajuda
Deus abençoe
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Qui Abr 17, 2014 17:42
por e8group » Qui Abr 17, 2014 17:42
Perdão ! Na correria acabei digitando errado . Vamos lá , sabemos que o termo da forma

vem da expressão
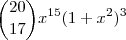
. Ao desenvolvermos
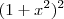
precisaremos de
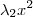
. Pois , produto de números de mesma base conserva a base e soma os expoentes . Logo o coef. será
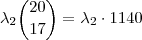
. Agora vamos determinar

.
Vamos utilizar o teorema binomial (será + rápido !!!)
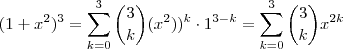
. Precisamos apenas de

. Assim , o nosso

é 3 , logo a resposta será
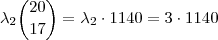
. Por favor , agora check a resposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Qui Abr 17, 2014 21:02
por Ovelha » Qui Abr 17, 2014 21:02
Muito obrigado, se você tiver um bom material de binômio estilo ita com questões resolvidas e comentadas. Aceito receber o link ou pdf para estudo,
Deus abençoe
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Qui Abr 17, 2014 22:07
por e8group » Qui Abr 17, 2014 22:07
De nada . Conheço um site que pode ser útil para vc :
http://www.rumoaoita.com/site/
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Sáb Abr 19, 2014 13:48
por Ovelha » Sáb Abr 19, 2014 13:48
Valeu pela dica. Agora desejo sabaer uma duvida. Ao escrever "Ao desenvolvermos
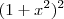
" na resposta os termos dentro doparenteses é elevado a 2 ou 3.
Obrigado
Deus abençoe
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Sáb Abr 19, 2014 14:00
por e8group » Sáb Abr 19, 2014 14:00
OMG , pensei certo e escrevi errado de novo .
O certo é ao desenvolvermos
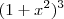
... . As potências de (x^2) serão sempre 0,1,2,3 . Todos naturais menores que 3 , Ou ainda , As potências de x serão 0,2,4,6 .
Lembre-se que ao desenvolver

cada parcela será da forma

com
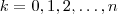
. Portanto , as potências de

são naturais variando de zero até n .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Sáb Abr 19, 2014 14:09
por Ovelha » Sáb Abr 19, 2014 14:09
Muito obrigADOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO.
DEUS ABENÇOE
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Binômio de Newton
por Giordane Junior » Sex Dez 03, 2010 00:46
- 0 Respostas
- 8106 Exibições
- Última mensagem por Giordane Junior

Sex Dez 03, 2010 00:46
Binômio de Newton
-
- (PUC-PR)BINOMIO DE NEWTON
por natanskt » Seg Dez 06, 2010 10:54
- 1 Respostas
- 7388 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 11:54
Binômio de Newton
-
- Binômio de Newton
por natanskt » Seg Dez 06, 2010 12:07
- 1 Respostas
- 8815 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:07
Binômio de Newton
-
- Binomio de Newton.
por 380625 » Sex Mar 11, 2011 12:57
- 1 Respostas
- 3022 Exibições
- Última mensagem por MarceloFantini

Sex Mar 11, 2011 16:20
Binômio de Newton
-
- Binomio de newton
 por Fabricio dalla » Sex Abr 01, 2011 01:13
por Fabricio dalla » Sex Abr 01, 2011 01:13
- 8 Respostas
- 8430 Exibições
- Última mensagem por LuizAquino

Sáb Jul 23, 2011 19:12
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 no desenvolvimento de
no desenvolvimento de 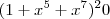

 no desenvolvimento de
no desenvolvimento de 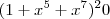

 em evidencia , teremos
em evidencia , teremos ![(1 + x^5 +x^7)^{20} = (1 +[x^5(1 +x^2)])^20 (1 + x^5 +x^7)^{20} = (1 +[x^5(1 +x^2)])^20](/latexrender/pictures/0ad7338f8254c716abb315c1a063622d.png) .Pelo teorema binomial ,
.Pelo teorema binomial ,![1 +[x^5(1 +x^2)])^20= \sum_{k=0}^{20} \binom{20}{k} [x^5(1+x^2)]^k = \sum_{k=0}^{20} \binom{20}{k} x^{5k}(1+x^2)^k = 1 + \binom{20}{1}x^5(1+x^2 ) + \binom{20}{2}x^{10}(1+x^2)^2 + \binom{20}{3}x^{15}(1 +x^2)^3 + \sum_{k=4}^{20} \binom{20}{k} [x^5(1+x^2)]^k 1 +[x^5(1 +x^2)])^20= \sum_{k=0}^{20} \binom{20}{k} [x^5(1+x^2)]^k = \sum_{k=0}^{20} \binom{20}{k} x^{5k}(1+x^2)^k = 1 + \binom{20}{1}x^5(1+x^2 ) + \binom{20}{2}x^{10}(1+x^2)^2 + \binom{20}{3}x^{15}(1 +x^2)^3 + \sum_{k=4}^{20} \binom{20}{k} [x^5(1+x^2)]^k](/latexrender/pictures/6b190677aa82f28ec474211533c54f62.png) .
. 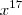 é oriundo da 4 parcela
é oriundo da 4 parcela  . Basta desenvolver para encontrar o coefc.
. Basta desenvolver para encontrar o coefc.  , o grau de x será sempre menor que
, o grau de x será sempre menor que  quando
quando  (afinal de contas
(afinal de contas 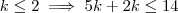 ) e maior que
) e maior que  quando
quando 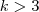 (afinal de contas
(afinal de contas 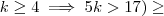 ) .
) .



 e
e  . O único termo que nos interessa é
. O único termo que nos interessa é  , pois
, pois 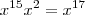 . Então o coefc. é
. Então o coefc. é 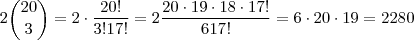 .
.

 vem da expressão
vem da expressão 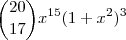 . Ao desenvolvermos
. Ao desenvolvermos 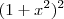 precisaremos de
precisaremos de 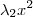 . Pois , produto de números de mesma base conserva a base e soma os expoentes . Logo o coef. será
. Pois , produto de números de mesma base conserva a base e soma os expoentes . Logo o coef. será 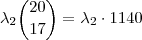 . Agora vamos determinar
. Agora vamos determinar  .
. 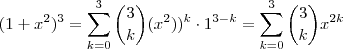 . Precisamos apenas de
. Precisamos apenas de  . Assim , o nosso
. Assim , o nosso  é 3 , logo a resposta será
é 3 , logo a resposta será 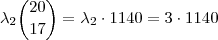 . Por favor , agora check a resposta .
. Por favor , agora check a resposta .


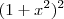 " na resposta os termos dentro doparenteses é elevado a 2 ou 3.
" na resposta os termos dentro doparenteses é elevado a 2 ou 3.
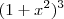 ... . As potências de (x^2) serão sempre 0,1,2,3 . Todos naturais menores que 3 , Ou ainda , As potências de x serão 0,2,4,6 .
... . As potências de (x^2) serão sempre 0,1,2,3 . Todos naturais menores que 3 , Ou ainda , As potências de x serão 0,2,4,6 .  cada parcela será da forma
cada parcela será da forma  com
com 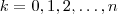 . Portanto , as potências de
. Portanto , as potências de  são naturais variando de zero até n .
são naturais variando de zero até n .

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.