 por thiagohp » Qui Nov 19, 2009 11:17
por thiagohp » Qui Nov 19, 2009 11:17
Vou dar uma resumida no problema.
É o seguinte:
Na questão tem um desenho com duas retas(R e S).Elas estão indicando nos seguintes pontos: (R)x=-2 e y=2, (S)x=2 e y=-1.
Com eu faço para descobrir aonde elas vao se cruzar em quais pontos x e y.
Obrigado.
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Nov 19, 2009 13:17
por Molina » Qui Nov 19, 2009 13:17
Boa tarde, Thiago.
Não tem como colocar a questão inteira (incluindo o desenho)?
Normalmente quando queremos descobrir onde duas retas se interceptam basta ter as duas equações que as geram e igualá-las. Com isso você descobre uma das coordenadas (digamos que x) e posteriormente substitui esse valor em qualquer das duas equações e descobre y.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por thiagohp » Qui Nov 19, 2009 13:29
por thiagohp » Qui Nov 19, 2009 13:29
Ok..Molina..colocarei o desenho.
O problema é que não consigo descobrir qual é o valor do coeficiente angular e nem saber direito qual a formula que uso para descobrir a equação das retas. No exercicio a figura esta toda quadriculada, mas só pelo desenho tentando unir as duas nao tem como descobrir aonde elas se encontram.(ate da aparentemente, mas não bate com o valor da alternativa correta).
Mas tudo bem...colocarei o desenho aqui para poder me ajudar.
Obrigado.
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Nov 19, 2009 13:39
por Molina » Qui Nov 19, 2009 13:39
Fórmula da reta:


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por thiagohp » Qui Nov 19, 2009 13:43
por thiagohp » Qui Nov 19, 2009 13:43
Então eu já usei esta ai....só q o problema é o coeficiente angular. Pelo o que eu sei a formula é assim né: m = Yb-Ya/Xb-Xa. certo?
Só que pra mim fazer esta formula eu preciso de outro ponto na reta e no exercicio só tem um ponto em cada reta e não dois.Entendeu?!
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sáb Nov 21, 2009 14:34
por Molina » Sáb Nov 21, 2009 14:34
thiagohp escreveu:Então eu já usei esta ai....só q o problema é o coeficiente angular. Pelo o que eu sei a formula é assim né: m = Yb-Ya/Xb-Xa. certo?
Só que pra mim fazer esta formula eu preciso de outro ponto na reta e no exercicio só tem um ponto em cada reta e não dois.Entendeu?!
Boa tarde!
Isso mesmo. Esse
m que você vai descobrir é o coeficiente angular.
Os pontos que o enunciado dá é
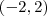
e

, sempre o primeiro elemento sendo
x e o segundo sendo
y..
Jogando na fórmula:
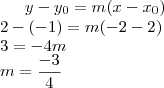
Consegue continuar agora?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por thiagohp » Sáb Nov 21, 2009 15:21
por thiagohp » Sáb Nov 21, 2009 15:21
Ok..entendi..mas eu não tenho que descobrir o coeficiente angular de cada reta?!!Neste caso vc descobriu um coeficiente angular usando os pontos de cada reta.
O desenho esta anexado a mensagem..de uma olhada por favor.
Obrigado.
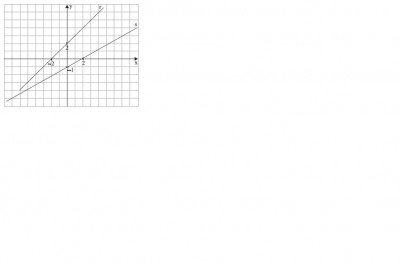
- Esta é a figura do exercicio.
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por thiagohp » Qui Nov 26, 2009 09:34
por thiagohp » Qui Nov 26, 2009 09:34
Por favor...alguem me ajude!!!
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por lucianofloripa » Qui Nov 26, 2009 11:43
por lucianofloripa » Qui Nov 26, 2009 11:43
THIAGO....suponho que com esse desenho, da para contar os quadradinho !!
ponto de intersecção é (-7,-5)
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
 por thiagohp » Qui Nov 26, 2009 12:15
por thiagohp » Qui Nov 26, 2009 12:15
Então foi o que eu imaginei, mas não.....a alternativa certa é (-6,-4).
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por lucianofloripa » Qui Nov 26, 2009 13:51
por lucianofloripa » Qui Nov 26, 2009 13:51
thiago ! a questão te induz a pensar que tem apenas 2 pontos como vc mencionou !
mas na verdade são 4: r (0,2) (-2,0) e s (2,0) (0,-1)
fazendo a matriz destes pontos, vc vai achar as equações 2x-2y+4=0 e x-2y-2=0
consegue continuar apartir dai ?
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
 por thiagohp » Qui Nov 26, 2009 14:09
por thiagohp » Qui Nov 26, 2009 14:09
Ahhh....entendi..cheguei na resposta..!!
Eu estava entendendo errado os pontos. Verdade, não tem dois pontos ai e sim 4..pois tanto a reta r e s não tem como ser um mesmo ponto os dois número que tem nelas. Pois se for ligar os pontos fica fora da reta.
Entendi....obrigado mesmo!! valeu...!
Obs: eu tenho uma duvida em um exercicio de logaritmo, em que parte aqui do forum eu coloco para que possam me ajudar?!
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por lucianofloripa » Qui Nov 26, 2009 14:14
por lucianofloripa » Qui Nov 26, 2009 14:14
não faço idéia, tbm sou novo aqui !!
vou nessa, abraço !
-
lucianofloripa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 20, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Arquitetura UFSC
- Andamento: formado
 por thiagohp » Qui Nov 26, 2009 14:31
por thiagohp » Qui Nov 26, 2009 14:31
Blz..valeu...e obrigado mais uma vez.
Abraço.
-
thiagohp
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Nov 19, 2009 11:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Interseção das retas
por Julia Capistrano » Seg Fev 28, 2011 20:49
- 4 Respostas
- 3957 Exibições
- Última mensagem por Julia Capistrano

Ter Mar 01, 2011 23:36
Geometria Plana
-
- Geometria analitica - Interseção de retas
por ubelima » Sáb Jun 02, 2012 23:21
- 3 Respostas
- 12626 Exibições
- Última mensagem por e8group

Sáb Out 06, 2012 10:37
Geometria Analítica
-
- Analítica - Interseção de retas e planos
por pedro_kampos » Qui Jul 24, 2014 23:49
- 1 Respostas
- 2428 Exibições
- Última mensagem por pedro_kampos

Dom Jul 27, 2014 20:59
Álgebra Linear
-
- Ângulo entre duas retas
por Jonatan » Qui Jul 22, 2010 13:38
- 0 Respostas
- 3587 Exibições
- Última mensagem por Jonatan

Qui Jul 22, 2010 13:38
Geometria Analítica
-
- enconto entre duas retas
por matematicada » Qua Nov 24, 2010 12:14
- 2 Respostas
- 1782 Exibições
- Última mensagem por alexandre32100

Qua Nov 24, 2010 12:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.










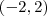 e
e  , sempre o primeiro elemento sendo x e o segundo sendo y..
, sempre o primeiro elemento sendo x e o segundo sendo y..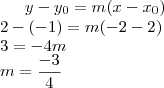










![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.