![g(x)= x\sqrt[]{8-x^2} g(x)= x\sqrt[]{8-x^2}](/latexrender/pictures/e8a3330ca09c0e12b4eae49c47c1c07e.png) . E tuda estava dando certo.
. E tuda estava dando certo.Derivei essa função e achei os pontos críticos, que são x=2 ou x=-2 e também
![x=2\sqrt[]{2} x=2\sqrt[]{2}](/latexrender/pictures/c22be52eb8f4f0951d1e50d52bfa1c09.png) ou
ou ![x=-2\sqrt[]{2} x=-2\sqrt[]{2}](/latexrender/pictures/19cf3cc91a175abf29a643f20739bf15.png)
Feito isso, eu derivei novamente essa função (no caso a segunda derivada) para verificar se os pontos críticos são pontos de máximo ou ponto de mínimo. E pelo que calculei, o x=2 é o ponto de máximo (segunda derivada é negativa) e também côncavo para baixo, e x=-2 é o ponto de mínimo (segunda derivada é positiva) e também côncavo para cima. Mas para
![x=2\sqrt[]{2} x=2\sqrt[]{2}](/latexrender/pictures/c22be52eb8f4f0951d1e50d52bfa1c09.png) e
e ![x=-2\sqrt[]{2} x=-2\sqrt[]{2}](/latexrender/pictures/19cf3cc91a175abf29a643f20739bf15.png) a segunda derivada não existe (joguei tudo pela calculadora pois é muito trabalho fazer tudo a mão), então não podemos afirmar nada se esses pontos são de máximo ou de mínimo. Mas eu sei que o x=0 é o ponto de inflexão, pois a segunda derivada é nula para esse ponto.
a segunda derivada não existe (joguei tudo pela calculadora pois é muito trabalho fazer tudo a mão), então não podemos afirmar nada se esses pontos são de máximo ou de mínimo. Mas eu sei que o x=0 é o ponto de inflexão, pois a segunda derivada é nula para esse ponto.OBS: deu muito trabalho para derivar essa função, pois é uma função polinominal junto com a raíz. Isso vira um jogo de regra da cadeia.
Feito isso eu esbocei o gráfico e ficou assim:
Mínimo local em x=-2 máximo local em x=2
Porém, o gabarito deu também que tem máximos e mínimos absolutos que é x=2 e x=-2 respectivamente, e máximo local em
![x=-2\sqrt[]{2} x=-2\sqrt[]{2}](/latexrender/pictures/19cf3cc91a175abf29a643f20739bf15.png) e mínimo local em
e mínimo local em ![x=2\sqrt[]{2} x=2\sqrt[]{2}](/latexrender/pictures/c22be52eb8f4f0951d1e50d52bfa1c09.png) , além de x=2 e x=-2 que achei. Eu não entendi o motivo da existência de extremos absolutos, transferi tudo para o software gráfico e esse gráfico ficou muito parecido com o meu, e o gabarito está dizendo que faltou alguma coisa. Alguém poderia me ajudar a verificar esse misterioso gráfico? Eu Agradeço se alguém puder
, além de x=2 e x=-2 que achei. Eu não entendi o motivo da existência de extremos absolutos, transferi tudo para o software gráfico e esse gráfico ficou muito parecido com o meu, e o gabarito está dizendo que faltou alguma coisa. Alguém poderia me ajudar a verificar esse misterioso gráfico? Eu Agradeço se alguém puder 
Abraço.


 é contínua no intervalo fechado
é contínua no intervalo fechado ![[-2\sqrt{2},2\sqrt{2}] = I [-2\sqrt{2},2\sqrt{2}] = I](/latexrender/pictures/9028607782c52a25f1db8c13519da1e9.png) (Este é o maior intervalo para o qual a função está definida) ,então pelo Teorema de Weierstrass está função possui um valor máximo absoluto e mínimo absoluto em
(Este é o maior intervalo para o qual a função está definida) ,então pelo Teorema de Weierstrass está função possui um valor máximo absoluto e mínimo absoluto em  .
.  são levados em imagem complexas por
são levados em imagem complexas por  .
.
![-2\sqrt[]{2} -2\sqrt[]{2}](/latexrender/pictures/bb6c4660bf6dc02d8eecc072ac83bf97.png) para
para ![2\sqrt[]{2} 2\sqrt[]{2}](/latexrender/pictures/202687598843121ee5b0808a42feb662.png) . Então quer dizer que os pontos críticos
. Então quer dizer que os pontos críticos  contendo um dos extremos do intervalo
contendo um dos extremos do intervalo  fosse ponto de máximo local de
fosse ponto de máximo local de 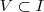 de
de 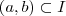 contendo
contendo  , mas acontece que não existe esta vizinhança
, mas acontece que não existe esta vizinhança  de
de 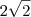 não é mínimo local .
não é mínimo local .