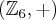 e o subconjunto
e o subconjunto  . Mostre que
. Mostre que  é um subgrupo de
é um subgrupo de 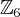 .
.Sei que para que J seja subgrupo de Z6, sei que J também deve ser um grupo que satisfaz a operação trabalhada nesse exercício. Mas não consigo mostrar o que se pede

Alguém sabe resolver?

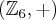 e o subconjunto
e o subconjunto  . Mostre que
. Mostre que  é um subgrupo de
é um subgrupo de 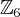 .
.

Cleyson007 escreveu:Considere o grupoe o subconjunto
. Mostre que
é um subgrupo de
.
Sei que para que J seja subgrupo de Z6, sei que J também deve ser um grupo que satisfaz a operação trabalhada nesse exercício. Mas não consigo mostrar o que se pede
Alguém sabe resolver?
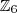 , temos que:
, temos que: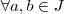 temos
temos 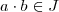
 existe
existe 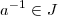
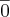 pois a operação é de soma, para 2 temos:
pois a operação é de soma, para 2 temos:
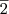 é o
é o  , logo temos o item 3.
, logo temos o item 3.

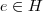
 tem-se
tem-se 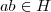 (aqui dizemos que H é fechado para a operação de G)
(aqui dizemos que H é fechado para a operação de G)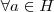 tem-se
tem-se 
 e
e  tem-se
tem-se  "
"


 é ou não é um subgrupo normal
é ou não é um subgrupo normal 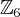 .
.
Cleyson007 escreveu:Renato,
Sem querer abusar de sua boa vontade, me ajuda nessa outra por favor:
Considerando esse mesmo exercício, verifique seé ou não é um subgrupo normal
.
Obrigado.
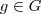 e
e 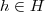 onde H é subgrupo de G (dizemos
onde H é subgrupo de G (dizemos 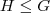 ), para que H seja subgrupo normal de G (
), para que H seja subgrupo normal de G ( ) temos que provar que:
) temos que provar que: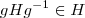 Para a operação.
Para a operação.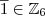 e
e 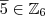 e seja
e seja 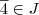 , logo:
, logo: Lembre-se que a operação soma é comutativa nos inteiros.
Lembre-se que a operação soma é comutativa nos inteiros. e
e 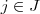 , logo:
, logo:


Cleyson007 escreveu:Renato,
e se me fosse pedido as classes laterais de J?
Obrigado.
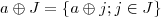
 , vamos pegar cada elemento de
, vamos pegar cada elemento de 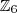 e somar (pois a operação do grupo é a soma) ao conjunto J, veja:
e somar (pois a operação do grupo é a soma) ao conjunto J, veja:

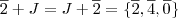
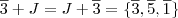
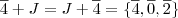

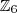 é abeliano (isto é,
é abeliano (isto é,  ).
).
 é um grupo". Como resolver?
é um grupo". Como resolver?
Cleyson007 escreveu:Renato, e se fosse pedido para comentar essa afirmação: "O conjuntoé um grupo". Como resolver?
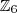 , portanto
, portanto  é um grupo quociente com a operação do grupo
é um grupo quociente com a operação do grupo 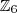 . Isso é uma proposição, para saber mais sobre ela consulte o livro Introdução à Álgebra do autor Adilson Gonçalves - SBM.
. Isso é uma proposição, para saber mais sobre ela consulte o livro Introdução à Álgebra do autor Adilson Gonçalves - SBM.




Cleyson007 escreveu:Boa noite Renato!
Sabe se encontro para baixar o livro Introdução à Álgebra do Adilson Gonçalves (Projeto Euclides - SBM)? Ou ebook do livro?
Agradeço,
Cleyson007

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)