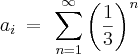
Mostre que (a?) é uma PG e determine seu termo geral.
Gabarito :
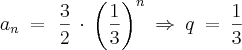
Obs: Não entendi o raciocínio usado para demonstrar que se trata de uma PG, e como determinar o termo geral.

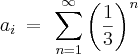
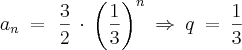

 ?
?


 . O termo geral será sempre da forma
. O termo geral será sempre da forma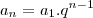
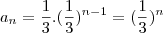

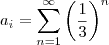 , todos os termos da sequência vão ser iguais a:
, todos os termos da sequência vão ser iguais a: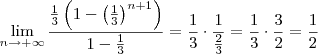

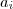 , verás que todos os termos serão iguais. Podemos considerar como uma PG, mas ela terá razão
, verás que todos os termos serão iguais. Podemos considerar como uma PG, mas ela terá razão  .
.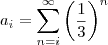 ?
?
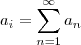
 e não
e não 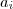 , é notável que
, é notável que  seja uma PG.
seja uma PG.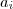 , na forma que aparece, não é uma sequência e sim uma série.
, na forma que aparece, não é uma sequência e sim uma série.
 na definição de
na definição de 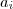 não tem relação nenhuma com o
não tem relação nenhuma com o  que aparece em
que aparece em  . São apenas variáveis, sem relação.
. São apenas variáveis, sem relação.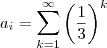

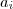 não é uma sequência, é uma série, mas não deixa de ser um TERMO da sequência
não é uma sequência, é uma série, mas não deixa de ser um TERMO da sequência 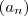 , ou seja, cada TERMO da sequência
, ou seja, cada TERMO da sequência 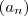 é uma série.
é uma série.
MateusL escreveu:Russmann, ona definição de
não tem relação nenhuma com o
que aparece em
. São apenas variáveis, sem relação.
Poderíamos dizer, para evitar confusão, que:
Apesar de eu achar que:

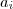 , a variável
, a variável  assume todos os valores inteiros de
assume todos os valores inteiros de  até o infinito?
até o infinito?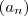 porque essa é a notação de sequência, indicando que os termos serão
porque essa é a notação de sequência, indicando que os termos serão  . Não há ligação entre esses
. Não há ligação entre esses  , eles apenas representam quantidades que variam.
, eles apenas representam quantidades que variam.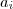 não é uma sequência, é uma série, mas não deixa de ser um TERMO da sequência
não é uma sequência, é uma série, mas não deixa de ser um TERMO da sequência 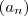 , ou seja, cada TERMO da sequência
, ou seja, cada TERMO da sequência 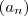 é uma série.
é uma série.
MateusL escreveu:Realmentenão é uma sequência, é uma série, mas não deixa de ser um TERMO da sequência
, ou seja, cada TERMO da sequência
é uma série.

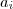 independe do valor de
independe do valor de  .
. .
.
MateusL escreveu:Com certeza o enunciado está confuso, mas tens que concordar comigo que, da forma que está, todos os termos serão iguais, porque a expressão que determina no termoindepende do valor de
.
Sendo assim, se resolvêssemos conforme está no enunciado, encontraríamos o termo geral constante e igual a.
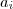 seja constante pois , obviamente, a série é convergente e independente de
seja constante pois , obviamente, a série é convergente e independente de  . Eu estou mais preocupado com o sentido do enunciado. kk
. Eu estou mais preocupado com o sentido do enunciado. kk
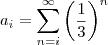


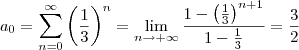
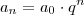 :
:

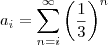

 cujo gabarito é (3/4)
cujo gabarito é (3/4)
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

