 , estou resolvendo uma função e ai surgil uma grande questão eu não sei canselar, pois a maneira como eu estou resolvendo, a resposta está dando diferente da do livro, a questão é:
, estou resolvendo uma função e ai surgil uma grande questão eu não sei canselar, pois a maneira como eu estou resolvendo, a resposta está dando diferente da do livro, a questão é:dada a função f(x)=ax+b, responda
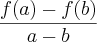 , onde
, onde 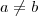 .
.Eu fiz assim:
 . Mas no gabarito a função da igual a a, gostaria que alguém iluminace minha mente para saber onde eu estou errando nessa bendita função. Desde já agradeço a atenção.
. Mas no gabarito a função da igual a a, gostaria que alguém iluminace minha mente para saber onde eu estou errando nessa bendita função. Desde já agradeço a atenção.

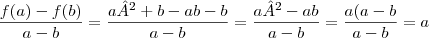
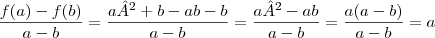


 .
.
 :
: