 por Thiago 86 » Seg Abr 15, 2013 21:36
por Thiago 86 » Seg Abr 15, 2013 21:36
Saldações

, estou resolvendo uma função e ai surgil uma grande questão eu não sei canselar, pois a maneira como eu estou resolvendo, a resposta está dando diferente da do livro, a questão é:
dada a função f(x)=ax+b, responda
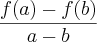
, onde
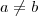
.
Eu fiz assim:

. Mas no gabarito a função da igual a a, gostaria que alguém iluminace minha mente para saber onde eu estou errando nessa bendita função. Desde já agradeço a atenção.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Victor Gabriel » Seg Abr 15, 2013 21:57
por Victor Gabriel » Seg Abr 15, 2013 21:57
irmão a resposta é assim:
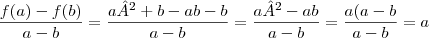
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Victor Gabriel » Seg Abr 15, 2013 21:59
por Victor Gabriel » Seg Abr 15, 2013 21:59
ai esta a resolução:
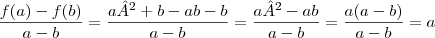
O A² NÃO TEM É a².
isto aA² não existe é só a².
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Thiago 86 » Ter Abr 16, 2013 15:06
por Thiago 86 » Ter Abr 16, 2013 15:06
Victor Gabriel escreveu:ai esta a resolução:
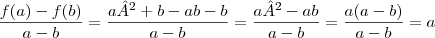
O A² NÃO TEM É a².
isto aA² não existe é só a².
Valeu por ter respondido minha questão.

Victor Gabriel, isso quer dizer que eu só posso canserlar o de baixo e o de cima quando for os dois de uma vez e o sinal do de baixo e do de cima baterem?
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , estou resolvendo uma função e ai surgil uma grande questão eu não sei canselar, pois a maneira como eu estou resolvendo, a resposta está dando diferente da do livro, a questão é:
, estou resolvendo uma função e ai surgil uma grande questão eu não sei canselar, pois a maneira como eu estou resolvendo, a resposta está dando diferente da do livro, a questão é: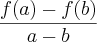 , onde
, onde 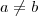 .
. . Mas no gabarito a função da igual a a, gostaria que alguém iluminace minha mente para saber onde eu estou errando nessa bendita função. Desde já agradeço a atenção.
. Mas no gabarito a função da igual a a, gostaria que alguém iluminace minha mente para saber onde eu estou errando nessa bendita função. Desde já agradeço a atenção.

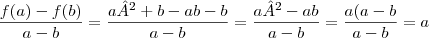
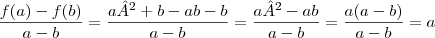


 , avisa que eu resolvo.
, avisa que eu resolvo.

