 por Douglas16 » Dom Mar 31, 2013 16:36
por Douglas16 » Dom Mar 31, 2013 16:36
Determinar os valores das constantes

e

de tal forma que
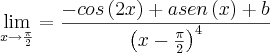
exista.
Depois, calcular o limite.
A única conclusão ou informação que consegui até agora é que b=-(a+1), isso vem do fato que para o valor limite existir, uma das condições é que tanto o limite do denominador quanto do numerador devem ser igual a zero, e a outra condição é a expressão seja tal que através do
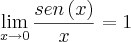
eu possa eliminar a indeterminação

, ou seja eliminar

.
Mas não vejo uma forma de fazer isso.
Tentei fazer a substituição:
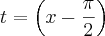
, mas ainda não vejo uma saída.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Douglas16 » Dom Mar 31, 2013 19:31
por Douglas16 » Dom Mar 31, 2013 19:31
A expressão do numerador pode ser fatorada como:
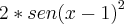
, admitindo x=-4.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 31, 2013 20:23
por e8group » Dom Mar 31, 2013 20:23
Considere :

quando
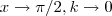
.
O limite a ser calculado será então :

ou

ou
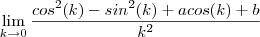
ou ainda ,
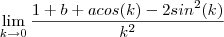
.
Mas,
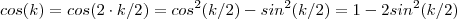
, então :

vemos então que o limite existe se ,e somente se ,

(Por quê ?)
Ou seja ,dado um

(ou

) real ,temos que

(ou

.) .Nestas condições o limite existirá .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Dom Mar 31, 2013 22:44
por Douglas16 » Dom Mar 31, 2013 22:44
Isso eu sei.
Mas considerando que a expressão do numerador pode ser fatorada como uma expressão quadrática em dois fatores:
Considerando X=

, tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1)
Logo vejo que o fator que possui a constante a, só zera quando a=-4 e usando este valor para encontrar o de b=3, sei que esse são os valores constantes, mas não sei como e porquê.
Para mim, o valor de a na expressão 1, deve ser tal que contenha o fator k^4, para eliminar a indeterminação.
Depois fazer a resolução para encontrar o valor limite.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 31, 2013 23:41
por e8group » Dom Mar 31, 2013 23:41
Na minha opinião ,sua solução não faz sentido ,qual finalidade de adotar este método ? Além do mais ,no denominador temos um polinômio enquanto no numerador não,portanto, não faz sentido a seguinte frase :
Douglas16 escreveu:Para mim, o valor de a na expressão 1, deve ser tal que contenha o fator k^4, para eliminar a indeterminação.
Depois fazer a resolução para encontrar o valor limite.
É isso ,caso dúvidas retorne .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Seg Abr 01, 2013 02:16
por Douglas16 » Seg Abr 01, 2013 02:16
Quanto ao polinômio, o correto é que eu teria de dizer: Deve-se eliminar a indeterminação

, eliminando ou assimilando por alguma identidade o termo

.
Agora veja se estou resolvendo corretamente:
Para que o limite exista:
(1)

(equação 1)
Portanto

,
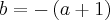
(equação 2)
(2) Deve-se eliminar a indeterminação

, eliminando ou assimilando por alguma identidade o termo

.
Fazendo a substituição da equação 2 na equação 1:

Fazendo X=

, tenho que:
2X²+

*X-

=(2X+a+2)(X-1) (equação 3)
Se X-1=

e

-1=
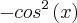
e
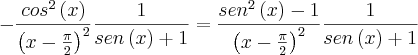
e de
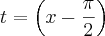
, portanto

(equação 4),
Portanto:
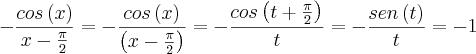
Assim (equação 3)/

, fica: [(2X+a+2)/
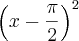
]*
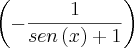
E para que o limite exista 2X+a+2=0 quando
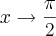
, portanto a=-4 e b=3.
Portanto o limite é
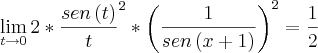
.
Concluindo:

e

. O valor do limite é

.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Seg Abr 01, 2013 13:31
por e8group » Seg Abr 01, 2013 13:31
Agora que observei que cometi um equívoco ,na verdade é
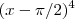
e não

,fazendo

fica no denominador
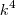
e não
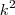
.Caso fosse

no denominador ,fixado
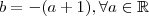
o limite sempre existiria, como mostra o wolframalpha :
http://www.wolframalpha.com/input/?i=li ... to++pi%2F2 , como não é o caso ,temos que impor mais condições sobre "a" e "b" .Peço desculpas pelo equívoco , parabéns pela dedicação a questão ,concluiu corretamente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 5153 Exibições
- Última mensagem por Russman

Ter Fev 25, 2014 02:17
Números Complexos
-
- constantes de proporcionalidades
por Fabricio dalla » Qui Mar 31, 2011 17:47
- 1 Respostas
- 1618 Exibições
- Última mensagem por Elcioschin

Qui Mar 31, 2011 19:09
Álgebra Elementar
-
- QUESTÃO INTEGRAL COM CONSTANTES!
por iel » Seg Jun 01, 2009 22:38
- 1 Respostas
- 3201 Exibições
- Última mensagem por Molina

Ter Jun 02, 2009 06:24
Cálculo: Limites, Derivadas e Integrais
-
- (Limites) Encontrar as constantes
 por Haahs » Qua Nov 04, 2009 00:32
por Haahs » Qua Nov 04, 2009 00:32
- 7 Respostas
- 6924 Exibições
- Última mensagem por Lucio Carvalho

Dom Abr 20, 2014 20:32
Cálculo
-
- Limites com constantes positivas
por EulaCarrara » Qua Abr 21, 2010 15:59
- 2 Respostas
- 2152 Exibições
- Última mensagem por MarceloFantini

Qua Abr 21, 2010 18:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  de tal forma que
de tal forma que 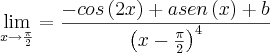 exista.
exista.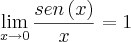 eu possa eliminar a indeterminação
eu possa eliminar a indeterminação  , ou seja eliminar
, ou seja eliminar  .
.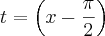 , mas ainda não vejo uma saída.
, mas ainda não vejo uma saída.

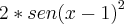 , admitindo x=-4.
, admitindo x=-4. quando
quando 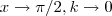 .
. ou
ou  ou
ou 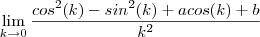 ou ainda ,
ou ainda , 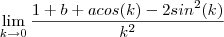 .
. 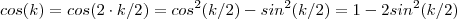 , então :
, então : 
 (Por quê ?)
(Por quê ?) (ou
(ou  .) .Nestas condições o limite existirá .
.) .Nestas condições o limite existirá .
 , tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1)
, tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1) (equação 1)
(equação 1) ,
, 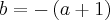 (equação 2)
(equação 2)
 =(2X+a+2)(X-1) (equação 3)
=(2X+a+2)(X-1) (equação 3) e
e  -1=
-1=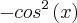 e
e 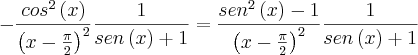
 (equação 4),
(equação 4),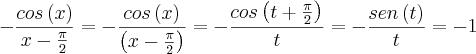
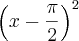 ]*
]*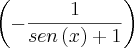
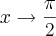 , portanto a=-4 e b=3.
, portanto a=-4 e b=3.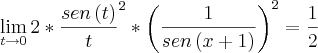 .
. e
e  . O valor do limite é
. O valor do limite é  .
.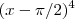 e não
e não  ,fazendo
,fazendo  fica no denominador
fica no denominador 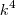 e não
e não 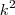 .Caso fosse
.Caso fosse 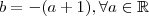 o limite sempre existiria, como mostra o wolframalpha :
o limite sempre existiria, como mostra o wolframalpha : ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.