 e
e  de tal forma que
de tal forma que 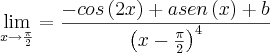 exista.
exista.Depois, calcular o limite.
A única conclusão ou informação que consegui até agora é que b=-(a+1), isso vem do fato que para o valor limite existir, uma das condições é que tanto o limite do denominador quanto do numerador devem ser igual a zero, e a outra condição é a expressão seja tal que através do
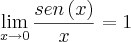 eu possa eliminar a indeterminação
eu possa eliminar a indeterminação  , ou seja eliminar
, ou seja eliminar  .
.Mas não vejo uma forma de fazer isso.
Tentei fazer a substituição:
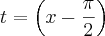 , mas ainda não vejo uma saída.
, mas ainda não vejo uma saída.

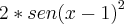 , admitindo x=-4.
, admitindo x=-4. quando
quando 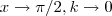 .
. ou
ou  ou
ou 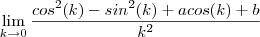 ou ainda ,
ou ainda , 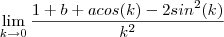 .
. 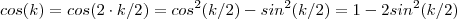 , então :
, então : 
 (Por quê ?)
(Por quê ?) (ou
(ou  .) .Nestas condições o limite existirá .
.) .Nestas condições o limite existirá .
 , tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1)
, tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1) (equação 1)
(equação 1) ,
, 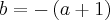 (equação 2)
(equação 2)
 =(2X+a+2)(X-1) (equação 3)
=(2X+a+2)(X-1) (equação 3) e
e  -1=
-1=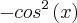 e
e 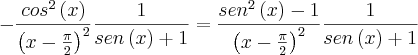
 (equação 4),
(equação 4),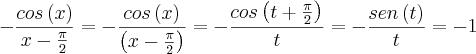
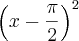 ]*
]*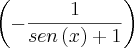
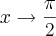 , portanto a=-4 e b=3.
, portanto a=-4 e b=3.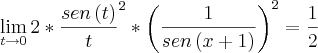 .
. e
e  . O valor do limite é
. O valor do limite é  .
.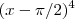 e não
e não  ,fazendo
,fazendo  fica no denominador
fica no denominador 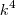 e não
e não 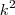 .Caso fosse
.Caso fosse 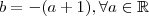 o limite sempre existiria, como mostra o wolframalpha :
o limite sempre existiria, como mostra o wolframalpha : ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)