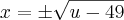por giboia90 » Ter Mar 19, 2013 18:40
por giboia90 » Ter Mar 19, 2013 18:40
queria duas forma de calcula
a integral de ;
![\int_{}^{}\sqrt[]{49+{x}^{2}} dx \int_{}^{}\sqrt[]{49+{x}^{2}} dx](/latexrender/pictures/71bedc225cd929d822402bc5a1d320f3.png)
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por marcosmuscul » Ter Mar 19, 2013 22:13
por marcosmuscul » Ter Mar 19, 2013 22:13
Será que é isso?

-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por nakagumahissao » Qua Mar 20, 2013 10:00
por nakagumahissao » Qua Mar 20, 2013 10:00
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por giboia90 » Qua Mar 20, 2013 10:07
por giboia90 » Qua Mar 20, 2013 10:07
valeu nakagumahissao
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por marcosmuscul » Qua Mar 20, 2013 14:27
por marcosmuscul » Qua Mar 20, 2013 14:27
ainda não comecei a faculdade, mas já estou estudando sozinho. Estou aqui no fórum pra aprender.
alguém poderia me explicar porque que da forma que eu fiz está errado. qual foi a regra que eu infringi?
obrigado.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por nakagumahissao » Qua Mar 20, 2013 15:29
por nakagumahissao » Qua Mar 20, 2013 15:29
marcosmuscul,
Ao mudar para

, você fez corretamente a derivação para:

, porém, ao substituir na Integral original, você transportou para debaixo da raiz o u, mas não passou o x reescrita em forma de 'u'. Ou seja, no caso em questão, como:

então,
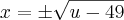
Desta maneira, se substituíssemos todos os x em forma de 'u', teríamos uma função muito mais difícil de ser integrada. Creio que o engano começou neste ponto.
Outras Observações: Não é permitido tirar 1/(2x) para fora da Integral pois x não é uma constante, independentemente do fato de não ter sido reescrito na forma em 'u', ou seja, utilizando em uma nova forma, cuja variável independente seja u ao invés de x.
Se eu estiver errado pessoal, por favor, me corrijam.
Acredito que esses são os pontos principais.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por marcosmuscul » Qua Mar 20, 2013 23:57
por marcosmuscul » Qua Mar 20, 2013 23:57
valeu pelo toque nakagumahissao.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\sqrt[]{49+{x}^{2}} dx \int_{}^{}\sqrt[]{49+{x}^{2}} dx](/latexrender/pictures/71bedc225cd929d822402bc5a1d320f3.png)

![\int_{}^{}\sqrt[]{49+{x}^{2}} dx \int_{}^{}\sqrt[]{49+{x}^{2}} dx](/latexrender/pictures/71bedc225cd929d822402bc5a1d320f3.png)



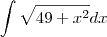
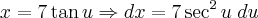


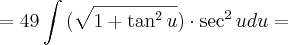
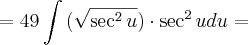
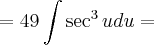






 , você fez corretamente a derivação para:
, você fez corretamente a derivação para: , porém, ao substituir na Integral original, você transportou para debaixo da raiz o u, mas não passou o x reescrita em forma de 'u'. Ou seja, no caso em questão, como:
, porém, ao substituir na Integral original, você transportou para debaixo da raiz o u, mas não passou o x reescrita em forma de 'u'. Ou seja, no caso em questão, como: