a integral de ;
![\int_{}^{}\sqrt[]{49+{x}^{2}} dx \int_{}^{}\sqrt[]{49+{x}^{2}} dx](/latexrender/pictures/71bedc225cd929d822402bc5a1d320f3.png)

![\int_{}^{}\sqrt[]{49+{x}^{2}} dx \int_{}^{}\sqrt[]{49+{x}^{2}} dx](/latexrender/pictures/71bedc225cd929d822402bc5a1d320f3.png)



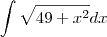
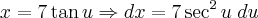


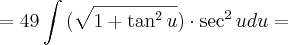
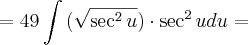
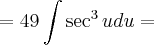






 , você fez corretamente a derivação para:
, você fez corretamente a derivação para: , porém, ao substituir na Integral original, você transportou para debaixo da raiz o u, mas não passou o x reescrita em forma de 'u'. Ou seja, no caso em questão, como:
, porém, ao substituir na Integral original, você transportou para debaixo da raiz o u, mas não passou o x reescrita em forma de 'u'. Ou seja, no caso em questão, como:
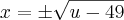


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.