a integral de ;
![\int_{}^{}\sqrt[]{49+{x}^{2}} dx \int_{}^{}\sqrt[]{49+{x}^{2}} dx](/latexrender/pictures/71bedc225cd929d822402bc5a1d320f3.png)

![\int_{}^{}\sqrt[]{49+{x}^{2}} dx \int_{}^{}\sqrt[]{49+{x}^{2}} dx](/latexrender/pictures/71bedc225cd929d822402bc5a1d320f3.png)



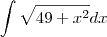
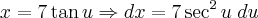


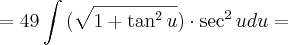
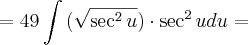
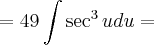






 , você fez corretamente a derivação para:
, você fez corretamente a derivação para: , porém, ao substituir na Integral original, você transportou para debaixo da raiz o u, mas não passou o x reescrita em forma de 'u'. Ou seja, no caso em questão, como:
, porém, ao substituir na Integral original, você transportou para debaixo da raiz o u, mas não passou o x reescrita em forma de 'u'. Ou seja, no caso em questão, como:
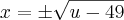


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)