 por thamysoares » Sex Nov 16, 2012 14:13
por thamysoares » Sex Nov 16, 2012 14:13
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sex Nov 16, 2012 14:52
por young_jedi » Sex Nov 16, 2012 14:52
a equação é

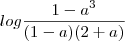
mais repare que
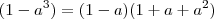
então
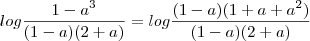
simplificando

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thamysoares » Sex Nov 16, 2012 15:10
por thamysoares » Sex Nov 16, 2012 15:10
young_jedi escreveu:a equação é

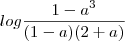
mais repare que
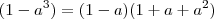
então
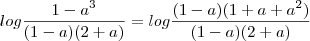
simplificando

Obigada, eu entendi o procedimento até aqui. Mas, como continua?
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sex Nov 16, 2012 15:20
por young_jedi » Sex Nov 16, 2012 15:20
daqui em diante não encontrei nenhuma maneria de simpificar mais
poderia ficar

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thamysoares » Sex Nov 16, 2012 15:42
por thamysoares » Sex Nov 16, 2012 15:42
young_jedi escreveu:daqui em diante não encontrei nenhuma maneria de simpificar mais
poderia ficar

As alternativas são 0, 1, 2 e log

=s
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sex Nov 16, 2012 16:39
por young_jedi » Sex Nov 16, 2012 16:39
não encontrei nenhuma maneira de chegar a uma destas alternativas...
verifique se o enunciado é este mesmo que voce postou, se não tem nada mais informando no exercicio
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thamysoares » Sex Nov 16, 2012 18:23
por thamysoares » Sex Nov 16, 2012 18:23
young_jedi escreveu:não encontrei nenhuma maneira de chegar a uma destas alternativas...
verifique se o enunciado é este mesmo que voce postou, se não tem nada mais informando no exercicio
Não vejo qual é o problema... Esta é uma questão da UFOP-MG e o enunciado diz somente "Ao simplificar a expressão obtém-se". Acabei de verificar e eu digitei corretamente a expressão. =/
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sex Nov 16, 2012 19:39
por young_jedi » Sex Nov 16, 2012 19:39
tem como voce me passar um link com a questão?
ai eu do uma olhada
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thamysoares » Sex Nov 16, 2012 20:13
por thamysoares » Sex Nov 16, 2012 20:13
young_jedi escreveu:tem como voce me passar um link com a questão?
ai eu do uma olhada
Desculpe, não encontrei na internet. Ela está na minha apostila de matemática feita pela minha própria escola. Mas ela está exatamente assim:
(UFOP-MG)Ao simplificar a expressão
![log(1-{a}^{3})-log(1-a)-log[(1+a)+1] log(1-{a}^{3})-log(1-a)-log[(1+a)+1]](/latexrender/pictures/7246a6235c5d971c4218c27b4512f88a.png)
obtém-se:
a) 0
b) 1
c) 2
d)

A não ser que contenha algum erro de digitação na apostila.
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sex Nov 16, 2012 21:06
por young_jedi » Sex Nov 16, 2012 21:06
obrigado tamysoares
verifiquei a questão e realmente não consegui chegar em nenhuma das respostas, talvez tenha algo que agente não esteja conseguindo visualizar, mas o mais provavel é que exista algum erro de digitação em sua apostila, se tiver como voce conferir com o pessoal que faz a apostila ou com algum professor é melhor.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thamysoares » Sáb Nov 17, 2012 09:36
por thamysoares » Sáb Nov 17, 2012 09:36
young_jedi escreveu:obrigado tamysoares
verifiquei a questão e realmente não consegui chegar em nenhuma das respostas, talvez tenha algo que agente não esteja conseguindo visualizar, mas o mais provavel é que exista algum erro de digitação em sua apostila, se tiver como voce conferir com o pessoal que faz a apostila ou com algum professor é melhor.
ok, muito obrigada =D
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2572 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1850 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2735 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5270 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2280 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![log(1-{a}^{3})-log(1-a)-log[(1+a)+1] log(1-{a}^{3})-log(1-a)-log[(1+a)+1]](/latexrender/pictures/7246a6235c5d971c4218c27b4512f88a.png)
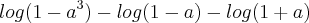
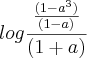
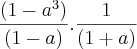


![log(1-{a}^{3})-log(1-a)-log[(1+a)+1] log(1-{a}^{3})-log(1-a)-log[(1+a)+1]](/latexrender/pictures/7246a6235c5d971c4218c27b4512f88a.png)
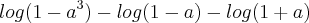
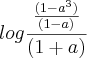
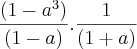



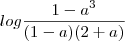
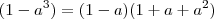
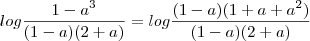





 =s
=s



![log(1-{a}^{3})-log(1-a)-log[(1+a)+1] log(1-{a}^{3})-log(1-a)-log[(1+a)+1]](/latexrender/pictures/7246a6235c5d971c4218c27b4512f88a.png) obtém-se:
obtém-se:


