Jhenrique escreveu:Comecei a relacionar todas as operações básicas e tentar compreedê-las, foi então que eu entendi de fato o que significa a parte literal de um monômio, ele é uma grandeza, na óptica da geometria, é um segmento de reta, logo, possui comprimento definido. Então, o produto de um segmento

por um

é a área

, porém, como o assunto é comprimento e comprimento é grandeza vetorial, pensei se o segmento

e o

, na verdade, não são vetores

e
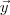
, respectivamente. Essa é a
1ª dúvida.
Em caso positivo, então porque o produto entre 2 vetores é diferente do produto entre 2 segmentos?
Em caso negativo, então o que vem a ser um segmento de comprimento

? É uma grandeza que cuja direção e sentido não importa, sendo importante apenas a magnitude, ou seja, é uma grandeza escalar?
Sim, é uma grandeza escalar. Apenas é necessário comprimento para caracterizar um segmento.
Jhenrique escreveu:2ª) Como posso diferenciar escalar de escalar? Em G.A., estuda-se o produto de um vetor (como a força, p ex) por um escalar (coeficente). Mas também existe o produto de um escalar (como a temperatura, p ex) por um escalar (coeficente), neste caso, como posso distinguir um do outro se eles recebem o mesmo nome?
Novamente, você quer misturar física e matemática fazendo os dois errados. Não se diferencia escalar de escalar, pelo menos se eles pertencerem ao mesmo
corpo (termo da álgebra abstrata). Um corpo é um conjunto com duas operações que satisfazem tudo que conhecemos: adição onde todo elemento tem inverso, existe elemento neutro, etc, e multiplicação para todo elemento não-nulo, com elemento identidade, associatividade, comutatividade, etc. De forma simples, exemplos de corpos são os racionais

, os reais

e os complexos

. Os inteiros

formam um anel, ou seja, não existe inverso multiplicativo para todo elemento. Inclusive, não é necessário nem identidade, associatividade e comutatividade, apenas a adição usual e a distributiva pela esquerda e pela direita.
Agora, o que você está falando envolve física, pois envolve unidades. Ora, normalmente trabalha-se com unidades como se trabalha com números normalmente, onde você só pode somar e subtrair mesmas unidades, porém é possível multiplicar e dividir unidades diferentes. Quando multiplicamos uma quantidade física por um número adimensional, normalmente este pode ser interpretado como uma dilatação ou contração da quantidade dita. Porém esta é uma interpretação física, não matemática.
Jhenrique escreveu:Outro exemplo:
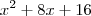
, aqui o
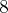
não é coeficente, o coeficente, na verdade, é

, e a parte literal é

,

dá a entender que está sendo somado
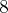
segmentos de medida

a uma área de

, o que não faz sentido, pois medida linear e quadrática são de gêneros diferentes.
E quanto a seguinte equação:
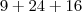
, será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?
Obg!
Começou, novamente, suas interpretações erradas. Os números que acompanham as potências são sempre os coeficientes, por definição. A "parte literal" é sempre a variável, por ser uma letra. Se você quer interpretar

, pense que você tem dois quadrados de lados

e 4, respectivamente. A área resultante do quadrado juntando-se ambos terá a área do primeiro,

, mais a área do segundo,

, mais um pedaço que é equivalente a

quando medido. Veja como a sua interpretação física falha gravemente pelo fato de você ignorar unidades e não ter regras consistentes para suas conclusões.
Soma de números é um número, simplesmente. Ou, nos termos acima, soma de escalares é um escalar. Sem você atribuir unidades, não é possível tirar significado desta soma. Como já disse anteriormente, só podemos somar ou subtrair unidades iguais, então se o primeiro for peso, o segundo tempo e o terceiro comprimento esta soma não existe fisicamente.
Como você já perguntou em tópicos anteriores: quer aprender matemática "de verdade"? Pare de atribuir estes significados e estude a coisa de uma forma mais abstrata.
 por um
por um  é a área
é a área  , porém, como o assunto é comprimento e comprimento é grandeza vetorial, pensei se o segmento
, porém, como o assunto é comprimento e comprimento é grandeza vetorial, pensei se o segmento  e o
e o  , na verdade, não são vetores
, na verdade, não são vetores  e
e  , respectivamente. Essa é a 1ª dúvida.
, respectivamente. Essa é a 1ª dúvida. ? É uma grandeza que cuja direção e sentido não importa, sendo importante apenas a magnitude, ou seja, é uma grandeza escalar?
? É uma grandeza que cuja direção e sentido não importa, sendo importante apenas a magnitude, ou seja, é uma grandeza escalar?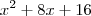 , aqui o
, aqui o  não é coeficente, o coeficente, na verdade, é
não é coeficente, o coeficente, na verdade, é  , e a parte literal é
, e a parte literal é  ,
,  dá a entender que está sendo somado
dá a entender que está sendo somado 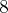 segmentos de medida
segmentos de medida  a uma área de
a uma área de  , o que não faz sentido, pois medida linear e quadrática são de gêneros diferentes.
, o que não faz sentido, pois medida linear e quadrática são de gêneros diferentes.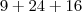 , será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?
, será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?

 , os reais
, os reais  e os complexos
e os complexos  . Os inteiros
. Os inteiros  formam um anel, ou seja, não existe inverso multiplicativo para todo elemento. Inclusive, não é necessário nem identidade, associatividade e comutatividade, apenas a adição usual e a distributiva pela esquerda e pela direita.
formam um anel, ou seja, não existe inverso multiplicativo para todo elemento. Inclusive, não é necessário nem identidade, associatividade e comutatividade, apenas a adição usual e a distributiva pela esquerda e pela direita.  , pense que você tem dois quadrados de lados
, pense que você tem dois quadrados de lados  , mais a área do segundo,
, mais a área do segundo,  , mais um pedaço que é equivalente a
, mais um pedaço que é equivalente a 

 e
e  , então a soma acima pode ser expressa pela equação
, então a soma acima pode ser expressa pela equação 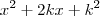 ou seja, é a soma de quadrados. Mas vc pode me dizer... "há como é que eu ia saber que vc tinha em mente um quadrado"... Poizé, hj eu já tenho 20 anos de idade, já resolvi muitas equações do 2º grau sem saber que as minhas contas faziam jus a um quadrado. Então eu comecei a perceber que na matemática e na geometria (
ou seja, é a soma de quadrados. Mas vc pode me dizer... "há como é que eu ia saber que vc tinha em mente um quadrado"... Poizé, hj eu já tenho 20 anos de idade, já resolvi muitas equações do 2º grau sem saber que as minhas contas faziam jus a um quadrado. Então eu comecei a perceber que na matemática e na geometria ( . Não! Não existem dimensões implícitas. Não assuma que existem. Isto está errado e não faz sentido.
. Não! Não existem dimensões implícitas. Não assuma que existem. Isto está errado e não faz sentido. ?
?
![y=1\times y\times \sqrt[dx]{dy}^x\times \sqrt[dx^2]{d^2y}^{x^2}\times ...\times \sqrt[dx^n]{d^ny}^{x^n} y=1\times y\times \sqrt[dx]{dy}^x\times \sqrt[dx^2]{d^2y}^{x^2}\times ...\times \sqrt[dx^n]{d^ny}^{x^n}](/latexrender/pictures/737b31686392a994f451d541dee9f751.png)
 , ou seja:
, ou seja: 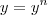 , que irá representar um problema ao substituir algebricamente a grandeza y por seu valor e unidade, então no primeiro membro teremos a unidade^1 e, no segundo, a mesma unidade^n !
, que irá representar um problema ao substituir algebricamente a grandeza y por seu valor e unidade, então no primeiro membro teremos a unidade^1 e, no segundo, a mesma unidade^n !