 por Jhenrique » Sáb Nov 10, 2012 18:57
por Jhenrique » Sáb Nov 10, 2012 18:57
Comecei a relacionar todas as operações básicas e tentar compreedê-las, foi então que eu entendi de fato o que significa a parte literal de um monômio, ele é uma grandeza, na óptica da geometria, é um segmento de reta, logo, possui comprimento definido. Então, o produto de um segmento

por um

é a área

, porém, como o assunto é comprimento e comprimento é grandeza vetorial, pensei se o segmento

e o

, na verdade, não são vetores

e
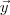
, respectivamente. Essa é a
1ª dúvida.
Em caso positivo, então porque o produto entre 2 vetores é diferente do produto entre 2 segmentos?
Em caso negativo, então o que vem a ser um segmento de comprimento

? É uma grandeza que cuja direção e sentido não importa, sendo importante apenas a magnitude, ou seja, é uma grandeza escalar?
2ª) Como posso diferenciar escalar de escalar? Em G.A., estuda-se o produto de um vetor (como a força, p ex) por um escalar (coeficente). Mas também existe o produto de um escalar (como a temperatura, p ex) por um escalar (coeficente), neste caso, como posso distinguir um do outro se eles recebem o mesmo nome?
Outro exemplo:
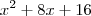
, aqui o
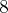
não é coeficente, o coeficente, na verdade, é

, e a parte literal é

,

dá a entender que está sendo somado
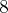
segmentos de medida

a uma área de

, o que não faz sentido, pois medida linear e quadrática são de gêneros diferentes.
E quanto a seguinte equação:
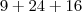
, será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?
Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sáb Nov 10, 2012 20:04
por MarceloFantini » Sáb Nov 10, 2012 20:04
Jhenrique escreveu:Comecei a relacionar todas as operações básicas e tentar compreedê-las, foi então que eu entendi de fato o que significa a parte literal de um monômio, ele é uma grandeza, na óptica da geometria, é um segmento de reta, logo, possui comprimento definido. Então, o produto de um segmento

por um

é a área

, porém, como o assunto é comprimento e comprimento é grandeza vetorial, pensei se o segmento

e o

, na verdade, não são vetores

e
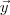
, respectivamente. Essa é a
1ª dúvida.
Em caso positivo, então porque o produto entre 2 vetores é diferente do produto entre 2 segmentos?
Em caso negativo, então o que vem a ser um segmento de comprimento

? É uma grandeza que cuja direção e sentido não importa, sendo importante apenas a magnitude, ou seja, é uma grandeza escalar?
Sim, é uma grandeza escalar. Apenas é necessário comprimento para caracterizar um segmento.
Jhenrique escreveu:2ª) Como posso diferenciar escalar de escalar? Em G.A., estuda-se o produto de um vetor (como a força, p ex) por um escalar (coeficente). Mas também existe o produto de um escalar (como a temperatura, p ex) por um escalar (coeficente), neste caso, como posso distinguir um do outro se eles recebem o mesmo nome?
Novamente, você quer misturar física e matemática fazendo os dois errados. Não se diferencia escalar de escalar, pelo menos se eles pertencerem ao mesmo
corpo (termo da álgebra abstrata). Um corpo é um conjunto com duas operações que satisfazem tudo que conhecemos: adição onde todo elemento tem inverso, existe elemento neutro, etc, e multiplicação para todo elemento não-nulo, com elemento identidade, associatividade, comutatividade, etc. De forma simples, exemplos de corpos são os racionais

, os reais

e os complexos

. Os inteiros

formam um anel, ou seja, não existe inverso multiplicativo para todo elemento. Inclusive, não é necessário nem identidade, associatividade e comutatividade, apenas a adição usual e a distributiva pela esquerda e pela direita.
Agora, o que você está falando envolve física, pois envolve unidades. Ora, normalmente trabalha-se com unidades como se trabalha com números normalmente, onde você só pode somar e subtrair mesmas unidades, porém é possível multiplicar e dividir unidades diferentes. Quando multiplicamos uma quantidade física por um número adimensional, normalmente este pode ser interpretado como uma dilatação ou contração da quantidade dita. Porém esta é uma interpretação física, não matemática.
Jhenrique escreveu:Outro exemplo:
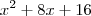
, aqui o
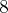
não é coeficente, o coeficente, na verdade, é

, e a parte literal é

,

dá a entender que está sendo somado
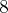
segmentos de medida

a uma área de

, o que não faz sentido, pois medida linear e quadrática são de gêneros diferentes.
E quanto a seguinte equação:
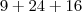
, será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?
Obg!
Começou, novamente, suas interpretações erradas. Os números que acompanham as potências são sempre os coeficientes, por definição. A "parte literal" é sempre a variável, por ser uma letra. Se você quer interpretar

, pense que você tem dois quadrados de lados

e 4, respectivamente. A área resultante do quadrado juntando-se ambos terá a área do primeiro,

, mais a área do segundo,

, mais um pedaço que é equivalente a

quando medido. Veja como a sua interpretação física falha gravemente pelo fato de você ignorar unidades e não ter regras consistentes para suas conclusões.
Soma de números é um número, simplesmente. Ou, nos termos acima, soma de escalares é um escalar. Sem você atribuir unidades, não é possível tirar significado desta soma. Como já disse anteriormente, só podemos somar ou subtrair unidades iguais, então se o primeiro for peso, o segundo tempo e o terceiro comprimento esta soma não existe fisicamente.
Como você já perguntou em tópicos anteriores: quer aprender matemática "de verdade"? Pare de atribuir estes significados e estude a coisa de uma forma mais abstrata.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sáb Nov 10, 2012 22:18
por Jhenrique » Sáb Nov 10, 2012 22:18
A própria geometria matemática trabalha com valores ao quadrado e ao cubo sem defenir unidade, não é falha minha, esta é a principal razão deste tópico: na matemática, quando eu vejo um número, eu só sei que ele é um escalar, mais nada, não sei se ele é adimensional, unidimensional, bidimensional, tridimensional ou uma mistura dimensional. É esta disinção dimensional que eu gostaria de saber se posso fazer e como fazer!!!
Outra coisa...
Já percebi que todo escalar não precisa estar associado necessariamente a uma unidade. Mas e o vetor? Todo vetor precisa estar associado necessariamente a uma unidade?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sáb Nov 10, 2012 22:22
por MarceloFantini » Sáb Nov 10, 2012 22:22
Nenhuma entidade matemática precisa estar associada a unidades.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Seg Nov 12, 2012 01:49
por Jhenrique » Seg Nov 12, 2012 01:49
Estou refletindo em tudo no que você está me dizendo. P ex, eu nunca havia percebido essa lei explicitamente.
MarceloFantini escreveu:só pode somar e subtrair mesmas unidades, porém é possível multiplicar e dividir unidades diferentes.
...
Jhenrique escreveu:E quanto a seguinte equação:
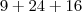
, será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?
MarceloFantini escreveu:[...]não é possível tirar significado desta soma. Como já disse anteriormente, só podemos somar ou subtrair unidades iguais[...]
Mas tipo... seja

e

, então a soma acima pode ser expressa pela equação
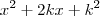
ou seja, é a soma de quadrados. Mas vc pode me dizer... "há como é que eu ia saber que vc tinha em mente um quadrado"... Poizé, hj eu já tenho 20 anos de idade, já resolvi muitas equações do 2º grau sem saber que as minhas contas faziam jus a um quadrado. Então eu comecei a perceber que na matemática e na geometria (
note que eu não estou falando de física e nem de unidades físicas), os números e as letras podem assumir dimensões implícitas, por exemplo, 25 pode ser 5 ao
quadrado. Então Marcelo, foi por isso que eu te perguntei se um escalar possui dimensão e se há alguma maneira de discerní-la com um olhar de raio-x.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Seg Nov 12, 2012 05:27
por MarceloFantini » Seg Nov 12, 2012 05:27
Jhenrique escreveu:Estou refletindo em tudo no que você está me dizendo. P ex, eu nunca havia percebido essa lei explicitamente.
MarceloFantini escreveu:só pode somar e subtrair mesmas unidades, porém é possível multiplicar e dividir unidades diferentes.
...
Esta é uma regra da física.
Jhenrique escreveu:Jhenrique escreveu:E quanto a seguinte equação:
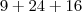
, será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?
MarceloFantini escreveu:[...]não é possível tirar significado desta soma. Como já disse anteriormente, só podemos somar ou subtrair unidades iguais[...]
Mas tipo... seja

e

, então a soma acima pode ser expressa pela equação
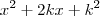
ou seja, é a soma de quadrados. Mas vc pode me dizer... "há como é que eu ia saber que vc tinha em mente um quadrado"... Poizé, hj eu já tenho 20 anos de idade, já resolvi muitas equações do 2º grau sem saber que as minhas contas faziam jus a um quadrado. Então eu comecei a perceber que na matemática e na geometria (
note que eu não estou falando de física e nem de unidades físicas), os números e as letras podem assumir dimensões implícitas, por exemplo, 25 pode ser 5 ao
quadrado. Então Marcelo, foi por isso que eu te perguntei se um escalar possui dimensão e se há alguma maneira de discerní-la com um olhar de raio-x.
Justamente pelo seu argumento que eu digo que não assumem dimensões implícitas, por poder ser escrito desta forma. Vamos supor que fosse metros. O que está querendo dizer é que

. Não! Não existem dimensões implícitas. Não assuma que existem. Isto está errado e não faz sentido.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Ter Nov 13, 2012 22:35
por Jhenrique » Ter Nov 13, 2012 22:35
As dimensões que eu estou me referindo seria com relação aos expoentes, a não com relação às unidades físicas.
Por exemplo... se vc afirma que a matemática ou os números ou a álgebra não assumuem dimensões, então porque um espaço tridimensional é definido como

?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qua Nov 14, 2012 07:39
por MarceloFantini » Qua Nov 14, 2012 07:39
Para responder à esta pergunta, eu sugiro que você estude álgebra linear.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Ter Jan 01, 2013 17:31
por Jhenrique » Ter Jan 01, 2013 17:31
Marcelo, eu queria deixa este tópico quietinho mas não dá, preciso perguntar pra desencargo de consciência!
Você afirmou que:
MarceloFantini escreveu:só pode somar e subtrair mesmas unidades, porém é possível multiplicar e dividir unidades diferentes.
E isso faz muito sentido quando analisamos as equações dimensionais de grandezas que variam segundo este modelo:

Mas nem todas as grandezas físicas ou abstratas variam conforme este modelo, mas podem variar assim também:
![y=1\times y\times \sqrt[dx]{dy}^x\times \sqrt[dx^2]{d^2y}^{x^2}\times ...\times \sqrt[dx^n]{d^ny}^{x^n} y=1\times y\times \sqrt[dx]{dy}^x\times \sqrt[dx^2]{d^2y}^{x^2}\times ...\times \sqrt[dx^n]{d^ny}^{x^n}](/latexrender/pictures/737b31686392a994f451d541dee9f751.png)
E ainda podem variar como a composição desses dois modelos com mais variáveis... mas deixa pra lá...
Enfim, como ficam as regras do jogo para o modelo acima?
É estranho... porque no final das contas fica que

, ou seja:
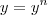
, que irá representar um problema ao substituir algebricamente a grandeza y por seu valor e unidade, então no primeiro membro teremos a unidade^1 e, no segundo, a mesma unidade^n !
Sem contar que o logaritmo entre duas grandezas é o primo da razão entre duas grandezas, no entanto, nunca vi ninguém calcular o logaritmo entre duas grandezas! E também tenho dúvidas de como ficaria a análise dimensional nesses casos.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda interpretação
por deividchou » Seg Ago 17, 2015 12:53
- 3 Respostas
- 4075 Exibições
- Última mensagem por AlexCA68

Sáb Mar 12, 2016 14:37
Aritmética
-
- Interpretação dessa questão
por Joelson » Dom Jun 21, 2009 17:22
- 2 Respostas
- 2934 Exibições
- Última mensagem por Joelson

Dom Jun 21, 2009 19:13
Álgebra Elementar
-
- Interpretação do enunciado Geometria
por opiniao » Qui Nov 01, 2012 11:29
- 3 Respostas
- 3322 Exibições
- Última mensagem por young_jedi

Qui Nov 01, 2012 14:10
Geometria Espacial
-
- [Limites] Interpretação de exercício
por Daniel Bosi » Seg Mai 16, 2016 22:20
- 2 Respostas
- 6107 Exibições
- Última mensagem por e8group

Qui Mai 19, 2016 20:27
Cálculo: Limites, Derivadas e Integrais
-
- Ambiguidade ou não na interpretaçao do exercicio
por Fabricio dalla » Dom Abr 02, 2023 02:39
- 1 Respostas
- 4009 Exibições
- Última mensagem por Fabricio dalla

Dom Abr 02, 2023 02:43
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 por um
por um  é a área
é a área  , porém, como o assunto é comprimento e comprimento é grandeza vetorial, pensei se o segmento
, porém, como o assunto é comprimento e comprimento é grandeza vetorial, pensei se o segmento  e o
e o  , na verdade, não são vetores
, na verdade, não são vetores  e
e 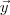 , respectivamente. Essa é a 1ª dúvida.
, respectivamente. Essa é a 1ª dúvida. ? É uma grandeza que cuja direção e sentido não importa, sendo importante apenas a magnitude, ou seja, é uma grandeza escalar?
? É uma grandeza que cuja direção e sentido não importa, sendo importante apenas a magnitude, ou seja, é uma grandeza escalar?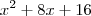 , aqui o
, aqui o 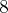 não é coeficente, o coeficente, na verdade, é
não é coeficente, o coeficente, na verdade, é  , e a parte literal é
, e a parte literal é  ,
,  dá a entender que está sendo somado
dá a entender que está sendo somado 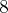 segmentos de medida
segmentos de medida  a uma área de
a uma área de  , o que não faz sentido, pois medida linear e quadrática são de gêneros diferentes.
, o que não faz sentido, pois medida linear e quadrática são de gêneros diferentes.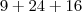 , será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?
, será que esses números representam a soma de áreas ou a soma de comprimentos ou a soma de coeficientes? Que me dizem?

 , os reais
, os reais  e os complexos
e os complexos  . Os inteiros
. Os inteiros  formam um anel, ou seja, não existe inverso multiplicativo para todo elemento. Inclusive, não é necessário nem identidade, associatividade e comutatividade, apenas a adição usual e a distributiva pela esquerda e pela direita.
formam um anel, ou seja, não existe inverso multiplicativo para todo elemento. Inclusive, não é necessário nem identidade, associatividade e comutatividade, apenas a adição usual e a distributiva pela esquerda e pela direita.  , pense que você tem dois quadrados de lados
, pense que você tem dois quadrados de lados  , mais a área do segundo,
, mais a área do segundo,  , mais um pedaço que é equivalente a
, mais um pedaço que é equivalente a 

 e
e  , então a soma acima pode ser expressa pela equação
, então a soma acima pode ser expressa pela equação 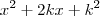 ou seja, é a soma de quadrados. Mas vc pode me dizer... "há como é que eu ia saber que vc tinha em mente um quadrado"... Poizé, hj eu já tenho 20 anos de idade, já resolvi muitas equações do 2º grau sem saber que as minhas contas faziam jus a um quadrado. Então eu comecei a perceber que na matemática e na geometria (
ou seja, é a soma de quadrados. Mas vc pode me dizer... "há como é que eu ia saber que vc tinha em mente um quadrado"... Poizé, hj eu já tenho 20 anos de idade, já resolvi muitas equações do 2º grau sem saber que as minhas contas faziam jus a um quadrado. Então eu comecei a perceber que na matemática e na geometria ( . Não! Não existem dimensões implícitas. Não assuma que existem. Isto está errado e não faz sentido.
. Não! Não existem dimensões implícitas. Não assuma que existem. Isto está errado e não faz sentido. ?
?
![y=1\times y\times \sqrt[dx]{dy}^x\times \sqrt[dx^2]{d^2y}^{x^2}\times ...\times \sqrt[dx^n]{d^ny}^{x^n} y=1\times y\times \sqrt[dx]{dy}^x\times \sqrt[dx^2]{d^2y}^{x^2}\times ...\times \sqrt[dx^n]{d^ny}^{x^n}](/latexrender/pictures/737b31686392a994f451d541dee9f751.png)
 , ou seja:
, ou seja: 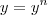 , que irá representar um problema ao substituir algebricamente a grandeza y por seu valor e unidade, então no primeiro membro teremos a unidade^1 e, no segundo, a mesma unidade^n !
, que irá representar um problema ao substituir algebricamente a grandeza y por seu valor e unidade, então no primeiro membro teremos a unidade^1 e, no segundo, a mesma unidade^n !