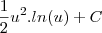por MrJuniorFerr » Seg Out 29, 2012 00:23
por MrJuniorFerr » Seg Out 29, 2012 00:23
Olá a todos, tentei resolver o seguinte exercício pelo método de substituição:


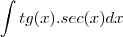
A partir daqui, fica claro que a integral de

, mas ainda sim, continuei a resolvê-lo pelo método de substituição.
Daí, coloquei

e
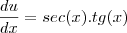
E fiz o seguinte:

, como podem ver, não alterei o resultado da integração.
Como

,
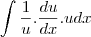
, cortando o

do numerador com o

do denominador:

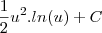

Ou seja, resultado incorreto...
O que eu fiz de errado?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por Russman » Seg Out 29, 2012 02:33
por Russman » Seg Out 29, 2012 02:33
Você simplificou errado o integrando:

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MrJuniorFerr » Seg Out 29, 2012 02:37
por MrJuniorFerr » Seg Out 29, 2012 02:37
Valeu Russman.
Pelo jeito então, deve-se simplificar ao máximo antes de integrar?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por Russman » Seg Out 29, 2012 03:09
por Russman » Seg Out 29, 2012 03:09
Poupa trabalho.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Seg Out 29, 2012 07:24
por MarceloFantini » Seg Out 29, 2012 07:24
Quero voltar a ressaltar que simplificar é sempre bom, mas em geral no resultado final. Existem simplificações que, dependendo da hora em que são feitos, mais atrapalham do que ajudam.
Em outras palavras Junior, não tente se agarrar à uma regra geral que resolverá todas as suas integrais. Isto não existe. Não sei se já ouviu esta frase clássica:
Derivar é técnico, integrar é arte.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Seg Out 29, 2012 07:37
por MrJuniorFerr » Seg Out 29, 2012 07:37
Bom dia Russman e Marcelo.
Entendi Marcelo. De fato, pude perceber que integrar é mais complexo que derivar...
Mas enfim, alguma conclusão com o que aconteceu eu tenho que tirar, e acho q a conclusão que eu tirei foi que é realmente necessário simplificar o integrando anteriormente a integração ou como você disse, no resultado final.
Valeu Marcelo!
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integrais] Problema com resolucao
 por gabrielnandi » Qui Jun 28, 2012 01:25
por gabrielnandi » Qui Jun 28, 2012 01:25
- 1 Respostas
- 1622 Exibições
- Última mensagem por Russman

Qui Jun 28, 2012 08:12
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Resolução incorreta?
por MrJuniorFerr » Dom Nov 11, 2012 23:04
- 4 Respostas
- 2595 Exibições
- Última mensagem por MrJuniorFerr

Seg Nov 12, 2012 20:34
Cálculo: Limites, Derivadas e Integrais
-
- Dois modos de falha
por rassis46 » Qui Abr 15, 2010 20:00
- 0 Respostas
- 1081 Exibições
- Última mensagem por rassis46

Qui Abr 15, 2010 20:00
Estatística
-
- [Integrais] Dúvida exercício
 por MrJuniorFerr » Dom Out 28, 2012 16:18
por MrJuniorFerr » Dom Out 28, 2012 16:18
- 8 Respostas
- 4322 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:38
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Dúvida exercício
por MrJuniorFerr » Dom Nov 11, 2012 10:51
- 5 Respostas
- 3520 Exibições
- Última mensagem por DanielFerreira

Dom Nov 11, 2012 13:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


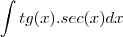
 , mas ainda sim, continuei a resolvê-lo pelo método de substituição.
, mas ainda sim, continuei a resolvê-lo pelo método de substituição. e
e 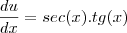
 , como podem ver, não alterei o resultado da integração.
, como podem ver, não alterei o resultado da integração. ,
,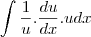 , cortando o
, cortando o  do numerador com o
do numerador com o  do denominador:
do denominador: