[Integrais] Exercício - resolução falha

por **MrJuniorFerr** » Seg Out 29, 2012 00:23

Olá a todos, tentei resolver o seguinte exercício pelo método de substituição:

$\int \frac{sen(x)}{cos^2(x)} dx$

$\int \frac{sen(x)}{cos(x)}.\frac{1}{cos(x)} dx$

$\int tg(x).sec(x) dx$

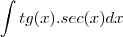
A partir daqui, fica claro que a integral de tg(x).sec(x) = sec(x) + C

, mas ainda sim, continuei a resolvê-lo pelo método de substituição.

Daí, coloquei u=sec(x)

e $\frac{du}{dx}=sec(x).tg(x)$

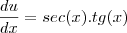
E fiz o seguinte:

$\int \frac{1}{sec(x)}.sec(x).tg(x).sec(x) dx$ , como podem ver, não alterei o resultado da integração.

Como u=sec(x)

,

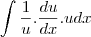$\int \frac{1}{u}.\frac{du}{dx}.u dx$ , cortando o

do numerador com o

do denominador:

$\int u.\frac{1}{u} du$

$\frac{1}{2}u^2.ln(u) + C$

$\frac{1}{2}sec^2x.ln(sec(x)) + C$

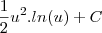
Ou seja, resultado incorreto...
O que eu fiz de errado?

por **Russman** » Seg Out 29, 2012 02:33

Você simplificou errado o integrando:

$\int u\frac{1}{u}du=\int du = u+C$

por **MrJuniorFerr** » Seg Out 29, 2012 02:37

Valeu Russman.
Pelo jeito então, deve-se simplificar ao máximo antes de integrar?

por **Russman** » Seg Out 29, 2012 03:09

Poupa trabalho.

por **MarceloFantini** » Seg Out 29, 2012 07:24

Quero voltar a ressaltar que simplificar é sempre bom, mas em geral no resultado final. Existem simplificações que, dependendo da hora em que são feitos, mais atrapalham do que ajudam.

Em outras palavras Junior, não tente se agarrar à uma regra geral que resolverá todas as suas integrais. Isto não existe. Não sei se já ouviu esta frase clássica:

Derivar é técnico, integrar é arte.

por **MrJuniorFerr** » Seg Out 29, 2012 07:37

Bom dia Russman e Marcelo.
Entendi Marcelo. De fato, pude perceber que integrar é mais complexo que derivar...
Mas enfim, alguma conclusão com o que aconteceu eu tenho que tirar, e acho q a conclusão que eu tirei foi que é realmente necessário simplificar o integrando anteriormente a integração ou como você disse, no resultado final.
Valeu Marcelo!

[Integrais] Exercício - resolução falha

[Integrais] Exercício - resolução falha

[Integrais] Exercício - resolução falha

Re: [Integrais] Exercício - resolução falha

Re: [Integrais] Exercício - resolução falha

Re: [Integrais] Exercício - resolução falha

Re: [Integrais] Exercício - resolução falha

Re: [Integrais] Exercício - resolução falha

Quem está online