 por MrJuniorFerr » Sex Out 12, 2012 11:51
por MrJuniorFerr » Sex Out 12, 2012 11:51
Tem um exercício aqui que estou com dúvida:
Obtenha a medida angular em radianos entre a reta r e o plano 

e
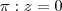
Sabe-se que para obter o ângulo de uma reta e um plano, deve-se utilizar esta fórmula:
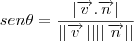
O vetor diretor
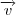
da reta é (0,1,-1) e o vetor normal
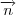
do plano é (0,0,1).
Apliquei na fórmula e cheguei que
![\theta=sen^-^1 \left(\frac{\sqrt[]{2}}{2} \right) \theta=sen^-^1 \left(\frac{\sqrt[]{2}}{2} \right)](/latexrender/pictures/4a5fc488da7c26d223dd99482b98f888.png)
Se eu fizesse a continha, daria 45º. Mas, o exercício quer em rad. Como eu faço isso?
Editando:
Ops, consegui fazer por regra de 3...
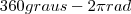
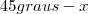
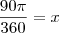
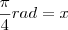
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Sex Out 12, 2012 12:44
por MarceloFantini » Sex Out 12, 2012 12:44
Uma observação: se você está usando o produto escalar (ou produto interno), então o resultado é o cosseno do ãngulo, não o seno.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Sex Out 12, 2012 13:13
por MrJuniorFerr » Sex Out 12, 2012 13:13
MarceloFantini escreveu:Uma observação: se você está usando o produto escalar (ou produto interno), então o resultado é o cosseno do ãngulo, não o seno.
É nada Marcelo, eu também imaginava que fosse assim devido as fórmulas do produto escalar e vetorial, pois o do produto escalar contém o cosseno e a do vetorial o seno. Mas de acordo com o livro
Geometria Analítica - Alfredo Steinbruch e com o gabarito da minha lista de exercícios, é da seguinte forma:
Quando queremos o ângulo de dois planos, devemos usar quase essa mesma fórmula que postei, só trocando o vetor diretor
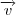
pelo vetor normal
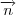
do outro plano e trocando o seno por cosseno e quando queremos o ângulo de uma reta e um plano, devemos essa fórmula que postei com o seno.
Lembrando que para os dois tipos de exercícios, se usam o produto escalar na fórmula. Realmente eu também acho estranho.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Sex Out 12, 2012 13:38
por MarceloFantini » Sex Out 12, 2012 13:38
Não faz sentido. Quando queremos o ângulo entre dois planos, apenas fazemos o produto escalar entre os vetores normais aos planos, logo
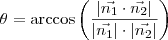
.
Se a reta e o vetor normal ao plano forem ortogonais o produto escalar entre eles será zero, que por sua fórmula indicará que o ângulo é zero entre eles, uma contradição. Você poderia citar o trecho em que o livro explica isto?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Sex Out 12, 2012 13:55
por MrJuniorFerr » Sex Out 12, 2012 13:55
Marcelo, to de saída agora.. vou até a universidade, pois combinei com a professora para tirar algumas dúvidas quanto a lista, pois a minha prova é na próxima terça. Ao voltar, coloco aqui todos os detalhes.
Até mais
Editando: No máximo 16:30 estou de volta.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MrJuniorFerr » Sex Out 12, 2012 18:53
por MrJuniorFerr » Sex Out 12, 2012 18:53
Desculpe a demora Marcelo, houve um imprevisto.
Tudo o que o livro diz sobre ângulo de retas e planos é:
Seja uma reta r com direção do vetor
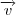
e um plano

, sendo
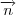
um vetor normal a

.
O ângulo

da reta r com o plano

é o complemento do ângulo

que a reta r forma com uma reta normal ao plano.
Tendo em vista que
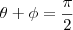
e, portanto,
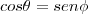
, vem, de acordo com a fórmula
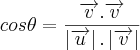
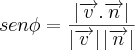
,
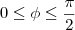
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Sex Out 12, 2012 20:18
por MarceloFantini » Sex Out 12, 2012 20:18
Agora tudo faz sentido.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ângulo entre reta e plano
por manuoliveira » Ter Mai 22, 2012 22:42
- 1 Respostas
- 2710 Exibições
- Última mensagem por LuizAquino

Qua Mai 23, 2012 20:16
Geometria Analítica
-
- [GA - Estudo da Reta] Exercício de GA com reta e plano
por matheus0807 » Qui Jun 05, 2014 15:12
- 0 Respostas
- 2108 Exibições
- Última mensagem por matheus0807

Qui Jun 05, 2014 15:12
Geometria Analítica
-
- [Dúvida reta e plano]
por Andresa_s » Qua Ago 01, 2012 13:02
- 1 Respostas
- 1600 Exibições
- Última mensagem por MarceloFantini

Qua Ago 01, 2012 21:07
Geometria Espacial
-
- [Interseção de reta e plano] Dúvida exerc.
por MrJuniorFerr » Dom Out 14, 2012 17:50
- 9 Respostas
- 4135 Exibições
- Última mensagem por MarceloFantini

Dom Out 14, 2012 22:38
Geometria Analítica
-
- [Interseção de reta e plano] Dúvida exerc. 2
por MrJuniorFerr » Seg Out 15, 2012 00:35
- 3 Respostas
- 2182 Exibições
- Última mensagem por MarceloFantini

Seg Out 15, 2012 08:13
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


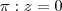

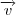 da reta é (0,1,-1) e o vetor normal
da reta é (0,1,-1) e o vetor normal 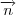 do plano é (0,0,1).
do plano é (0,0,1).![\theta=sen^-^1 \left(\frac{\sqrt[]{2}}{2} \right) \theta=sen^-^1 \left(\frac{\sqrt[]{2}}{2} \right)](/latexrender/pictures/4a5fc488da7c26d223dd99482b98f888.png)
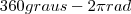
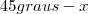
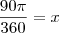
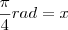




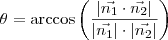 .
. da reta r com o plano
da reta r com o plano  que a reta r forma com uma reta normal ao plano.
que a reta r forma com uma reta normal ao plano.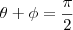 e, portanto,
e, portanto, 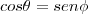 , vem, de acordo com a fórmula
, vem, de acordo com a fórmula 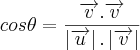
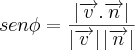 ,
,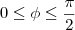
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
