"conhece-se, há mais de um século, uma fórmula para expressar o peso ideal do corpo humano adulto em função da altura:
P =
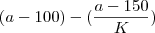
onde P é o peso, em quilos, a é a altura, em centímetros, k = 4, para homens, e k = 2, para mulheres".
a) Cíntia, que pesa 54 quilos, fez rapidamente as contas com k = 2 e constatou que, segundo a fórmula, estava 3 quilos abaixo do seu peso ideal. Calcule a altura de Cíntia.
b) Paulo e Paula têm a mesma altura e ficaram felizes em saber que estavam ambos exatamente com seu peso ideal, segundo a informação da revista. Sabendo que Paulo pesa 2 quilos a mais do que Paula, determine o peso de cada um deles.
Gostaria de saber o raciocinio e o desenvolvimento da conta.






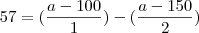
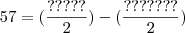 - Fiquei em duvida nessa parte, que eu sei é dividir em baixo e multiplicar em cima.
- Fiquei em duvida nessa parte, que eu sei é dividir em baixo e multiplicar em cima.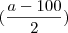
 =
=  Seria isso o resultado da fração do Primeiro ?
Seria isso o resultado da fração do Primeiro ?
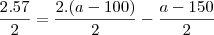
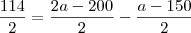

 ?
?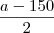 , voce não precisa mexer pois ele ja esta no denominador 2, ja nos outros termos voce tem que "mexer", multiplicando e dividindo eles por dois, voce não altera eles mais coloca eles no mesmo denominador.
, voce não precisa mexer pois ele ja esta no denominador 2, ja nos outros termos voce tem que "mexer", multiplicando e dividindo eles por dois, voce não altera eles mais coloca eles no mesmo denominador.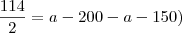 --- Duvida aqui, se eu dividi o
--- Duvida aqui, se eu dividi o  , teria que dividi todos os termos da direita certo ?
, teria que dividi todos os termos da direita certo ?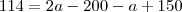
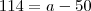


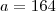
 e
e 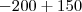 diretamente né, não moveu nenhum dos dois ?
diretamente né, não moveu nenhum dos dois ?![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.