 por replay » Qua Out 10, 2012 21:37
por replay » Qua Out 10, 2012 21:37
7 (UFRJ) Cintia, Paulo e Paula leram a seguinte informação numa revista:
"conhece-se, há mais de um século, uma fórmula para expressar o peso ideal do corpo humano adulto em função da altura:
P =
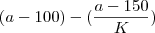
onde P é o peso, em quilos,
a é a altura, em centímetros, k = 4, para homens, e k = 2, para mulheres".
a) Cíntia, que pesa 54 quilos, fez rapidamente as contas com k = 2 e constatou que, segundo a fórmula, estava 3 quilos abaixo do seu peso ideal. Calcule a altura de Cíntia.
b) Paulo e Paula têm a mesma altura e ficaram felizes em saber que estavam ambos exatamente com seu peso ideal, segundo a informação da revista. Sabendo que Paulo pesa 2 quilos a mais do que Paula, determine o peso de cada um deles.
Gostaria de saber o raciocinio e o desenvolvimento da conta.
Editado pela última vez por
replay em Qui Out 11, 2012 16:30, em um total de 1 vez.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por jeanderson09 » Qua Out 10, 2012 21:53
por jeanderson09 » Qua Out 10, 2012 21:53
olha..... quando vc se inscreve no site fica bem claro que o objetivo dos usuarios nao e responder questoes e fazer perguntas , mas sim discutir os metodos de resoluçao.....

-
jeanderson09
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Out 10, 2012 20:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qua Out 10, 2012 22:07
por replay » Qua Out 10, 2012 22:07
Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios, trabalhos, provas etc.
Caso você não tenha tentado algo pois ainda não sabe como iniciar o exercício, então informe essa dificuldade.
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo;
Sempre que eu posto algo, eu posto o desenvolvimento da conta, no caso eu não sei como iniciar o calculo.
O intuito do forum é o aprender e não resolver questões, respeito muito a politica do forum.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qui Out 11, 2012 16:29
por replay » Qui Out 11, 2012 16:29
Substituindo os termos eu fiz:
54 =

Como não tem nada embaixo do a - 100 eu coloquei 1 para fazer a conta.
Estou fazendo certo ?
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Out 11, 2012 17:20
por young_jedi » Qui Out 11, 2012 17:20
A formula relaciona o peso ideal a altura, no enunciado de a) diz que cintia esta 3 kg abaixo de seu peso ideal, ou seja o peso ideal de Cintia seria 57 Kg, portanto voce tem que usar este valor na formula.
Corrigindo isso, voce montou a formula certa, e sim, voce pode colocar o 1 no denominador, agora é so aplicar o minimo multiplo comum e resolver.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por replay » Qui Out 11, 2012 17:39
por replay » Qui Out 11, 2012 17:39
Young_Jedi.
Percebo que estou com bastante dificuldade nesse tipo de equação, poderia completa-la ?
Consegui até montar essa parte:
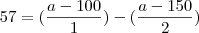
Retirando o MMC:
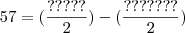
- Fiquei em duvida nessa parte, que eu sei é dividir em baixo e multiplicar em cima.
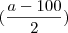

=

Seria isso o resultado da fração do Primeiro ?
(Dividindo por 2 em baixo) e multiplicando em cima.
Outra coisa que vejo: Esse tipo de equação não foi ensinado na escola(Rede Estadual).
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Out 11, 2012 18:27
por young_jedi » Qui Out 11, 2012 18:27
o mmc é 2
então o denominador de todas as parcelas tem que ser igual a dois
para isso voce multiplica e divide todas as parcelas por dois, para não alterar seu valor.

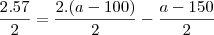
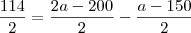
como todo a equação tem o mesmo denominador então podemos igualar o numerador e trabalhas so com esse

Comentarios: com relação a sua queixa do ensino desse tipo de equação na escola, isso depende muito, ja ouvi varias pessoas falarem disto, mais por exemplo eu estudei em rede estadual e isto foi estudado nas escolas que frequentei, depende muito de cidade, estado, escola e principalmente professor.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por replay » Qui Out 11, 2012 19:33
por replay » Qui Out 11, 2012 19:33
Deixa eu ver se eu entendi, não precisava tirar o MMC?
Ja que eu poderia multiplicar e dividir por 2, isso faria com que eu tivesse uma equivalência em

?
Seria isso ou minha dedução ta errada?
Outra coisa que vejo, estou tendo muita dificuldade em matematica, e pretendo ser engenheiro, essa dificuldade vai atrapalhar ?
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Out 11, 2012 20:03
por young_jedi » Qui Out 11, 2012 20:03
Na verdade o mmc é 2, nesse caso é facil verificar porque os outros termos estão divididos por um
o objetivo de tirar o mmc é deixar todos os termos no mesmo denominador e assim igualar os numeradores
o termo
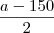
, voce não precisa mexer pois ele ja esta no denominador 2, ja nos outros termos voce tem que "mexer", multiplicando e dividindo eles por dois, voce não altera eles mais coloca eles no mesmo denominador.
com relação a outra duvida, bom, eu te digo que matematica é essencial para um bom engenheiro, se voce esta tendo dificuldade recomendo que estudo bastante, pois uma boa base matematica é fundamental na faculdade de engenharia e na vida profissional do engenheiro. O importante é ter empenho e não desanimar.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por replay » Qui Out 11, 2012 20:52
por replay » Qui Out 11, 2012 20:52
Tentei desenvolver a ultima conta, não consegui.
Seria separar numero com numero e letra com letra ?
Pode desenvolve-la ?
Eu fiz assim:

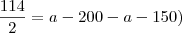
--- Duvida aqui, se eu dividi o

, teria que dividi todos os termos da direita certo ?
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qui Out 11, 2012 21:19
por replay » Qui Out 11, 2012 21:19
É isso mesmo você acertou a questão.

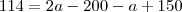
Você fez

e
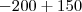
diretamente né, não moveu nenhum dos dois ?
As vezes fico um pouco constrangido de fazer perguntas sucetivas, mais eu tentei antes de fazer a pergunta, é que não consegui mesmo.
Engraçado, uma coisa, eu não vejo nada de "função", apenas equação de primeiro grau.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Out 11, 2012 21:29
por young_jedi » Qui Out 11, 2012 21:29
isso, eu fiz a conta direto sem organizar os termos
o exercicio te da uma função do peso pela altura P(a) a partir do momento que voce tem o valor de um dos dois
ou do peso ou da altura, voce substitui na função ai voce tera uma equação para encontrar o valor do outro
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de Função (UFRJ)
por Carolziiinhaaah » Qui Ago 12, 2010 11:34
- 1 Respostas
- 2731 Exibições
- Última mensagem por Douglasm

Qui Ago 12, 2010 13:14
Funções
-
- (UFRJ 2009 ) Questão do vestibular da ufrj em 2009 me ajudem
por rafael84 » Ter Jul 13, 2010 22:57
- 1 Respostas
- 2585 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 15, 2010 01:28
Binômio de Newton
-
- Questão da Ufrj
por 321 » Ter Ago 31, 2010 02:32
- 0 Respostas
- 2871 Exibições
- Última mensagem por 321

Ter Ago 31, 2010 02:32
Matrizes e Determinantes
-
- Questão concurso UFRJ
por sun123+ » Qui Dez 11, 2014 19:22
- 1 Respostas
- 1496 Exibições
- Última mensagem por nakagumahissao

Sex Dez 12, 2014 19:42
Equações
-
- (UFRJ) Função
por aline2010 » Qui Jun 17, 2010 20:43
- 1 Respostas
- 1292 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 20:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
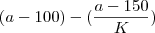






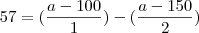
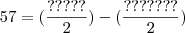 - Fiquei em duvida nessa parte, que eu sei é dividir em baixo e multiplicar em cima.
- Fiquei em duvida nessa parte, que eu sei é dividir em baixo e multiplicar em cima.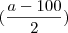
 =
=  Seria isso o resultado da fração do Primeiro ?
Seria isso o resultado da fração do Primeiro ?
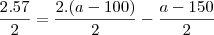
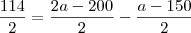

 ?
?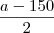 , voce não precisa mexer pois ele ja esta no denominador 2, ja nos outros termos voce tem que "mexer", multiplicando e dividindo eles por dois, voce não altera eles mais coloca eles no mesmo denominador.
, voce não precisa mexer pois ele ja esta no denominador 2, ja nos outros termos voce tem que "mexer", multiplicando e dividindo eles por dois, voce não altera eles mais coloca eles no mesmo denominador.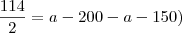 --- Duvida aqui, se eu dividi o
--- Duvida aqui, se eu dividi o  , teria que dividi todos os termos da direita certo ?
, teria que dividi todos os termos da direita certo ?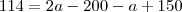
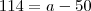


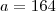
 e
e 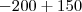 diretamente né, não moveu nenhum dos dois ?
diretamente né, não moveu nenhum dos dois ?

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.