 e
e  são dois números reais e
são dois números reais e 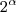 = m e
= m e 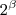 = n, então
= n, então 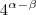 é igual a:
é igual a:Já tentei mas, pelo visto, eu tenho que saber quanto é
 e
e  para depois subtrair
para depois subtrair  -
- 

 e
e  são dois números reais e
são dois números reais e 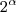 = m e
= m e 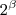 = n, então
= n, então 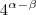 é igual a:
é igual a: e
e  para depois subtrair
para depois subtrair  -
- 




Bielto escreveu:Eu já assisti todas as vídeo aulas sobre potenciação, já resolvi vários exercícios (só os fáceis) e mesmo assim.
Eu pélo para resolver um exercício, como esse apresentado. Eu já li as teorias em livros, conheço todas as propriedades da potenciação

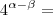
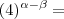
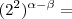
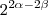
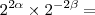
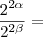
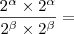
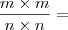
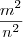

Arkanus Darondra escreveu:
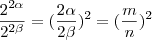


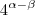 =
= 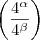 São recíprocas?
São recíprocas?


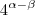 =
= 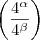 São recíprocas de qual propriedade?
São recíprocas de qual propriedade?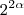 x
x 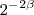 ? É a recíproca do que? ou de qual propriedade?
? É a recíproca do que? ou de qual propriedade?
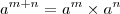 e
e 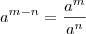 , sendo que
, sendo que  é um número maior que zero. Normalmente as pessoas aprendem a usar "em um sentido apenas", ou seja, quando tem potências multiplicando elas somam e quando tem potências dividindo subtraem. Isto é reforçado por uma bateria de exercício em que apenas isso é feito.
é um número maior que zero. Normalmente as pessoas aprendem a usar "em um sentido apenas", ou seja, quando tem potências multiplicando elas somam e quando tem potências dividindo subtraem. Isto é reforçado por uma bateria de exercício em que apenas isso é feito. 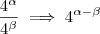 , e a recíproca é verdadeira,
, e a recíproca é verdadeira, 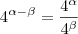 .
.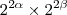 foi primeiro usada a propriedade que
foi primeiro usada a propriedade que 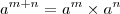 .
.

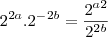 o por quê? Que o sinal do b passou para baixo positivo?
o por quê? Que o sinal do b passou para baixo positivo? 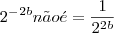

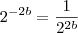 . Perceba que
. Perceba que 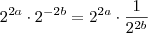 , mas quando multiplicamos uma fração com numerador um por alguma coisa, escrevemos essa alguma coisa dividida pelo denominador, daí
, mas quando multiplicamos uma fração com numerador um por alguma coisa, escrevemos essa alguma coisa dividida pelo denominador, daí 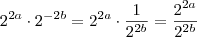 .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

